các trường hợp bằng nhau của tam giác vuông:Bài tập các trường hợp bằng nhau của tam giác vuông.
Chắc hẳn các em cũng đã xem qua đề thi vào 10 của các anh chị 2k4 năm nay để đạt điểm 7-8 là không khó, tuy nhiên trong đề thi có vài điểm đánh lừa, dễ gây sai sót khi làm bài. ✅ Chính vì thế cần phải nắm chắc kiến thức, hiểu rõ bản chất để làm chắc bài, không bị mất điểm .
Mục tiêu
Lý thuyết cần nhớ
Các dạng bài tập
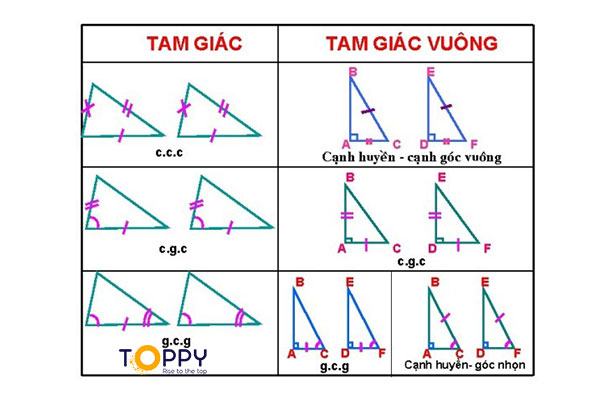
Một Số sơ đồ tư duy các trường hợp bằng nhau của tam giác vuông:
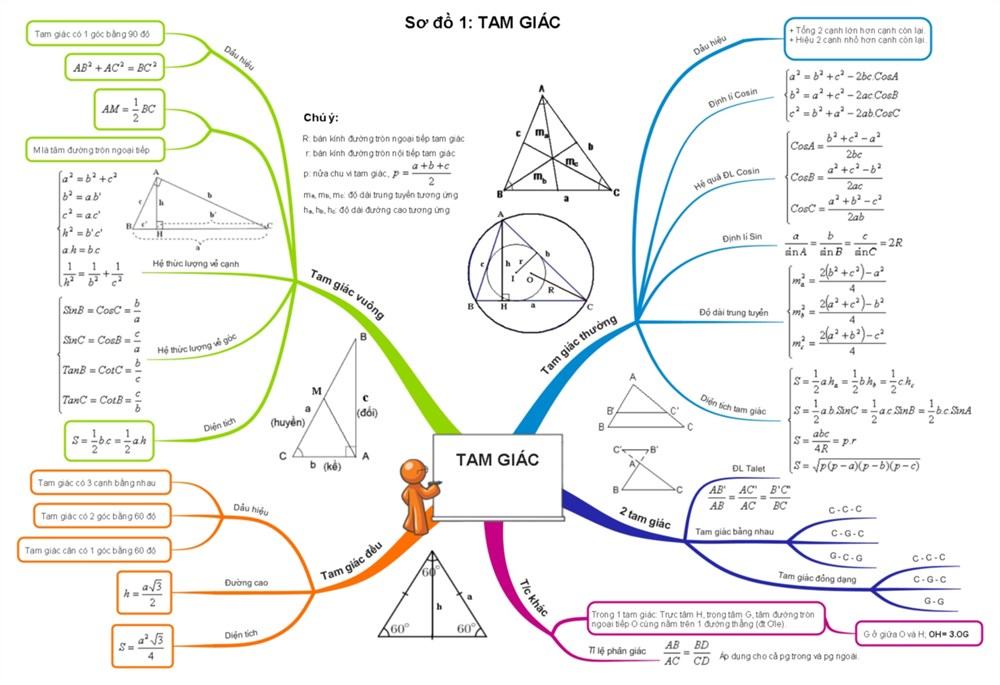
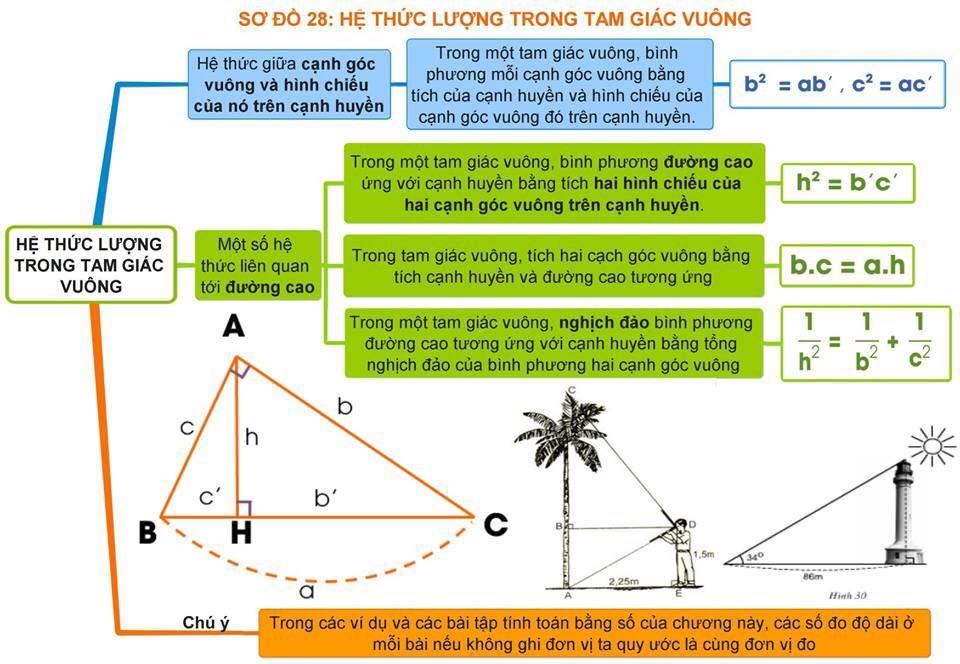
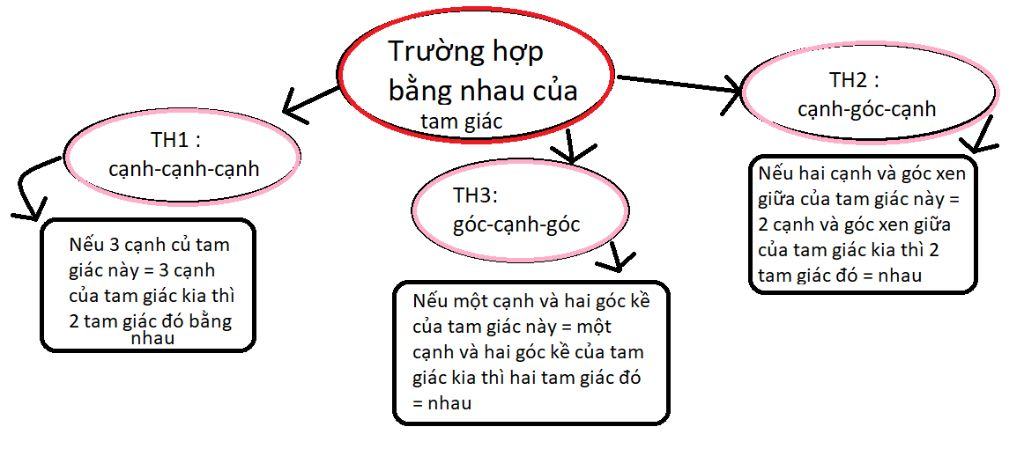
Các kiến thức và dạng bài tập các trường hợp 2 tam giác bằng nhau
I. Các kiến thức cần nhớ
1. Nhắc lại các trường hợp bằng nhau đã biết
+ Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh-góc-cạnh).
+ Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (góc-cạnh-góc).
+ Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh huyền – góc nhọn)
2. Trường hợp bằng nhau cạnh huyền và cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau.
![]()
II. Các dạng toán thường gặp
Dạng 1: Tìm hoặc chứng minh hai tam giác vuông bằng nhau
Phương pháp:
– Xét hai tam giác vuông
– Kiểm tra các điều kiện bằng nhau cạnh-góc-cạnh, góc-cạnh-góc, cạnh huyền-góc nhọn, cạnh huyền-cạnh góc vuông.
– Kết luận hai tam giác bằng nhau
Dạng 2: Chứng minh các đoạn thẳng bằng nhau, các góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc.
Phương pháp:
+ Chọn hai tam giác vuông có các yếu tố cần tính hoặc chứng minh.
+ Chứng minh hai tam giác vuông đó bằng nhau theo một trong các trường hợp đã học
+ Suy ra các cạnh (góc) tương ứng bằng nhau và kết luận.
Bài tập về các trường hợp bằng nhau của tam giác
Câu hỏi trắc nghiệm
Bài 1: Cho tam giác ABC và tam giác NPM có BC = PM, ∠B = ∠P = 90° . Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh huyền – cạnh góc vuông?
A. BA = PM B. BA = PN C. CA = MN D. ∠A = ∠N
Ta có hai tam giác ABC và tam giác NPM có BC = PM, ∠B = ∠P = 90° mà BC, PM là hai cạnh góc vuông của tam giác ABC và NPM nên để hai tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông thì ta cần thêm điều kiện CA = MN
Chọn đáp án C.
Bài 2: Cho tam giác ABC và tam giác MNP có ∠A = ∠M = 90°, ∠C = ∠P. Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề?
A. AC = MP B. AB = MN C. BC = NP D. AC = MN
Ta có: ∠C = ∠P mà góc C và góc P là hai góc nhọn kề của tam giác ABC và tam giác MNP
Do đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh hóc vuông – góc nhọn kề thì cần thêm điều kiện AC = MP
Chọn đáp án A.
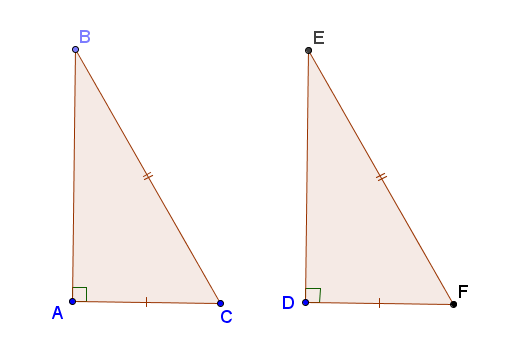
Bài 3: Cho tam giác ABC và tam giác DEF có: ∠B = ∠E = 90°, AC = DF, ∠A = ∠F. Phát biểu nào sau đây đúng?
A. ΔABC = ΔFED
B. ΔABC = ΔFDE
C. ΔBAC = ΔFED
D. ΔABC = ΔDEF
Xét tam giác ABC và tam giác FED có:
![]()
Suy ra ΔABC = ΔFED
Chọn đáp án A.
Bài 4: Cho tam giác ABC và tam giác KHI có: ∠A = ∠K = 90°, AB = KH, BC = HI. Phát biểu nào sau đây đúng?
A. ΔABC = ΔKHI
B. ΔABC = ΔHKI
C. ΔABC = ΔKIH
D. ΔACB = ΔKHI
Xét tam giác ABC và tam giác KHI có:
∠A = ∠K = 90°, AB = KH, BC = HI
⇒ ΔABC = ΔKHI
Chọn đáp án A
Bài 5: Cho tam giác ABC và tam giác DEF có AB = DE, ∠B = ∠E, ∠A = ∠D = 90°. Biết AC = 9cm. Tính độ dài DF?
A. 10cm B. 5cm C. 9cm D. 7cm
Xét tam giác ABC và tam giác DEF có:
![]()
⇒ ΔABC = ΔDEF. Khi đó AC = DF = 9cm
Chọn đáp án C
Bài 1: Cho tam giác ABC vuông tại A, phân giác BE (Điểm E thuộc cạnh AC), đường thẳng qua E vuông góc với BC tại D và cắt tia BA tại F
a. Chứng minh hai tam giác EAB và EDB bằng nhau.
b. So sánh EA và EC va chứng minh EC = EF
c. Gọi O là giao điểm của đường thẳng BE và CE. Chứng minh OA = OD
Bài 2: Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh hai tam giác ABM và ACM bằng nhau.
b) Chứng minh AM vuông góc BC.
c) Chứng minh AM là phân giác của góc A
Chứng minh rằng:
a. ∆ABD = ∆ACD
b. ∆DBE = ∆DCH
c. ∆ABH = ∆ACE
Bài 4: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy điểm H sao cho BH = BA.
a) Chứng minh ∆ABD = ∆HBD
b) Chứng minh DH vuông góc với BC
c) Giả sử góc . Tính số đo góc ADB
Bài 5: cho tam giác ABC vuông tại B, đường phân giác AD (D thuộc BC). Kẻ BO vuông góc với AD (O thuộc AD), BO cắt AC tại E. Chứng minh:
a. ∆ABO = ∆AEO
b. ∆BAE cân
c. AD là đường trung trực của BE
d. Kẻ BK vuông góc với AC (K ∈ AC). Gọi M là giao điểm của BK và AD. Chứng minh rằng ME// BC
Bài tập các trường hợp bằng nhau của tam giác vuông

Bài viết khác cùng mục: