Các trường hợp bằng nhau của tam giác vuông

Hai tam giác vuông bằng nhau khi: cạnh huyền và cạnh góc vuông tương ứng bằng nhau (trường hợp đặc biệt), hoặc cạnh huyền và góc nhọn tương ứng bằng nhau, hoặc hai cạnh góc vuông tương ứng bằng nhau, hoặc cạnh góc vuông và góc nhọn kề tương ứng bằng nhau

Định nghĩa hai tam giác bằng nhau

Khi 2 hình tam giác giống nhau về hình dạng và kích thước thì chúng bằng nhau. Nói cách khác, hai hình này có độ dài 3 cạnh tương ứng bằng nhau và số đo của 3 góc tương ứng bằng nhau.

Để ký hiệu hai tam giác ABC và DEF bằng nhau, ta có thể viết là △ABC = △DEF. Ký hiệu này có nghĩa là như sau:

• Các cạnh tương ứng AB = DE, BC = EF và AC = DF.
• Các góc tương ứng ∠BAC = ∠EDF, ∠ABC = ∠DEF và ∠BCA = ∠EFD.

Các trường hợp bằng nhau của hai tam giác vuông

Theo chương trình SGK Toán lớp 7, tam giác vuông là tam giác có một góc vuông, tức là một góc bằng 90 độ. Trong tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền, hai cạnh còn lại gọi là cạnh góc vuông.

Ví dụ: Tam giác ABC vuông tại A nghĩa là ∠A = 90°, khi đó cạnh BC là cạnh huyền, còn AB và AC là hai cạnh góc vuông.

Để xác định hai tam giác vuông có bằng nhau hay không, ta cần dựa vào các yếu tố quan trọng như cạnh và góc. Trong hình học, có 4 trường hợp bằng nhau của tam giác vuông, hãy tìm hiểu chi tiết cùng Sforum ngay sau đây:

Hai cạnh góc vuông

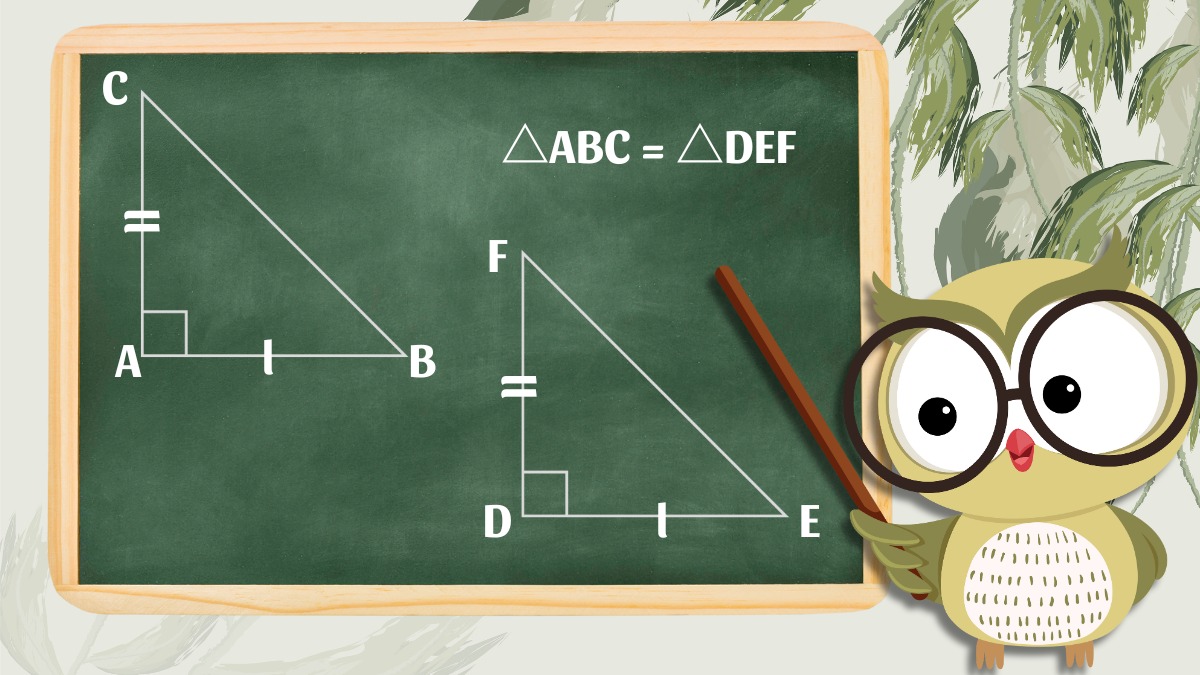
Nếu hai tam giác vuông có 2 cặp cạnh góc vuông có chiều dài bằng nhau thì ta có thể khẳng định rằng chúng bằng nhau. Trong 4 trường hợp bằng nhau của tam giác vuông, trường hợp này được gọi là cạnh – góc – cạnh (c-g-c). Ví dụ, nếu △ABC vuông tại A và △DEF vuông tại D có AB = DE, AC = DF thì hai tam giác này hoàn toàn bằng nhau, ta có ký hiệu là △ABC = △DEF.

Cạnh góc vuông và góc nhọn liền kề cạnh đó

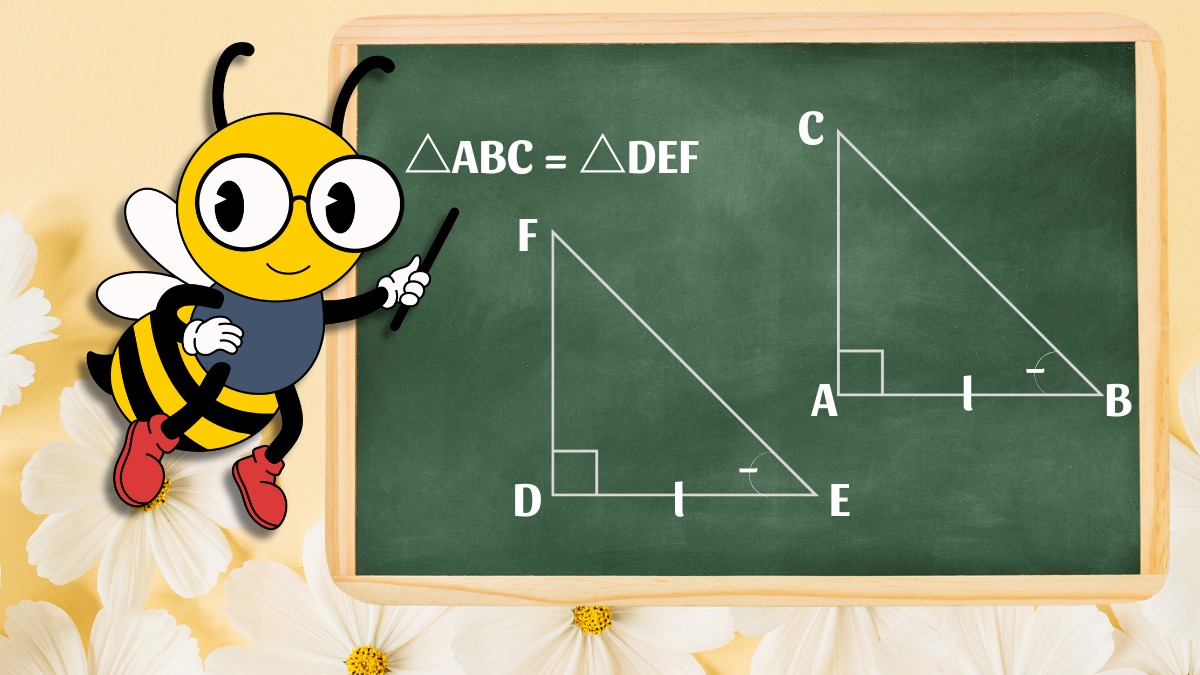
Hai tam giác vuông được coi là bằng nhau nếu chúng có 2 cạnh góc vuông tương ứng bằng nhau và 2 góc nhọn kề 2 cạnh đó cũng bằng nhau. Đây là trường hợp góc – cạnh – góc (g-c-g) trong chứng minh tam giác. Nhờ nguyên tắc này, ta có thể chứng minh hai tam giác vuông bằng nhau mà không cần so sánh toàn bộ ba cạnh. Ví dụ, nếu △ABC vuông tại A và △DEF vuông tại D có AB = DE và ∠ABC = ∠DEF thì △ABC = △DEF.