Phiếu bài tập tam giác cân lớp 7 file word có lời giải

Phiếu bài tập tam giác cân lớp 7 file word có lời giải.

Mục tiêu

1. Cách chứng minh tam giác cân

Để chứng minh một tam giác là tam giác cân ta sử dụng một trong hai cách sau:

– Cách 1: Chứng minh tam giác đó có hai cạnh bằng nhau.

– Cách 2: Chứng minh tam giác đó có hai góc bằng nhau.

Xem ví dụ dưới đây để nắm được cách chứng minh tam giác cân.

Ví dụ: Trong tam giác ABC có ΔABM = ΔACM . Chứng minh tam giác ABC cân.

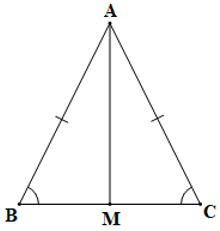
+ Chứng minh theo cách 1:

Theo bài ra, ta có:

ΔABM = ΔACM

⇒ AB = AC

⇒ Tam giác ABC cân tại A

+ Chứng minh theo cách 2:

Theo bài ra, ta có:

∆ABM = ∆ACM

⇒ Góc B = C

⇒ Tam giác ABC cân tại A

2. Định nghĩa tam giác cân

Tam giác cân là tam giác có 2 cạnh bên bằng nhau.

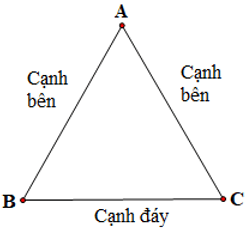
Từ hình vẽ, ta xác định được:

– Đỉnh A của tam giác cân ABC là giao điểm của hai cạnh bên AB và AC.

– Góc A được gọi là góc ở đỉnh, hai góc còn lại B và C là góc đáy.

3. Cách dựng tam giác ABC cân tại A

– Vẽ cạnh BC

– Vẽ cung tròn tâm B, bán kính r

– Vẽ cung tròn tâm C, bán kính r

+ Hai cung tròn cắt nhau tại A.

+ Tam giác ABC là tam giác cần vẽ.

4. Tính chất của tam giác cân

– Tính chất 1: Trong tam giác cân, hai góc đáy bằng nhau.

Ví dụ: Tam giác ABC cân tại A ⇒ Góc B = C

– Tính chất 2: Tam giác có hai góc bằng nhau là tam giác cân.

Ví dụ: Tam giác ABC có góc B = C ⇒ Tam giác ABC cân tại A

– Tính chất 3: Trường hợp đặc biệt của tam giác cân:

Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

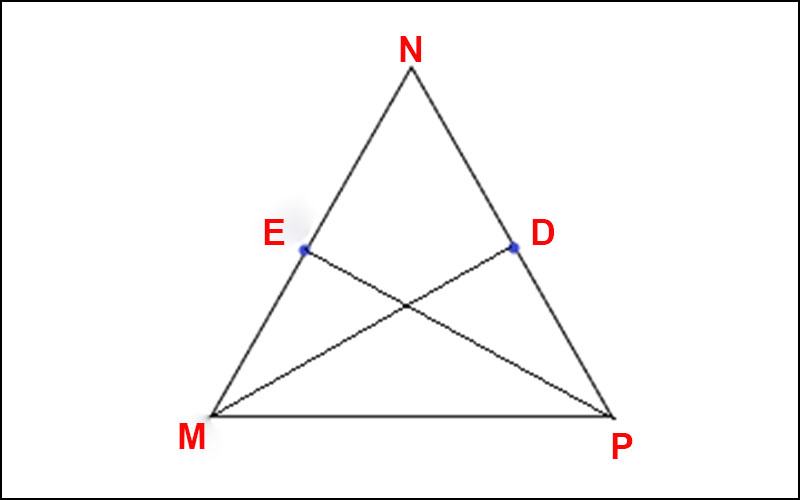
Ví dụ: Tam giác MNP vuông tại M có góc N = P ⇒ Tam giác MNP vuông cân tại M

Tính số đo mỗi góc nhọn của tam giác vuông cân.

Ta có: Δ ABC có Góc A = 90°, Góc B = C

⇒ Góc B + C = 90° (định lí tổng ba góc của một tam giác)

⇒ 2.Ĉ = 90°

⇒ Góc B = C = 45°

Kết luận: Tam giác vuông cân thì hai góc nhọn bằng 45°.

5. Bài tập áp dụng các cách chứng minh tam giác cân

Bài 1: Trong các tam giác ở các hình 15a, b, c, d, tam giác nào là tam giác cân, tam giác nào là tam giác đều ? Vì sao ?

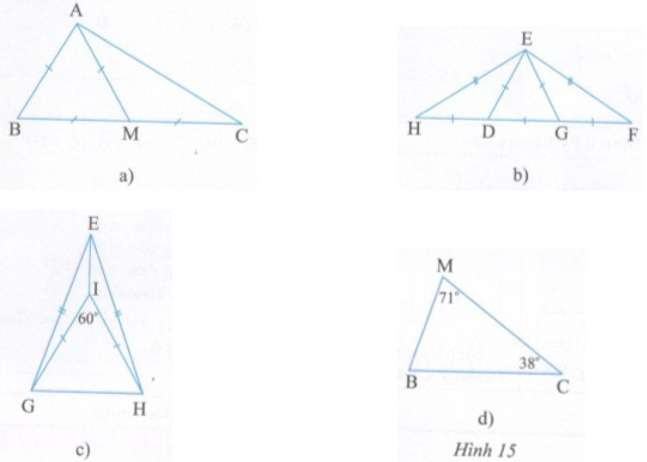
Giải:

a) Ta có: AB = BM = AM (gt) => tam giác ABM đều.

AM = CM (gt) => tam giác MAC cân tại M.

b) Ta có: ED = DG = EG (gt) => tam giác EDG đều.

DH = DE => tam giác DEH cân tại D.

Ta có: EG = GF => tam giác GEF cân tại G.

Ta có: EH = EF => tam giác EHF cân tại E.

c) Ta có: IG = IH (gt) => tam giác IGH cân tại I. Mà góc GIH=60^o (gt). Do đó tam giác IGH đều.

Ta có: EG = EH (gt) => tam giác EGH cân tại E.

d) Tam giác MBC có: góc M + góc B+góc C=180^o

Do đó: 71^o + góc B = 38^o = 180^o =>Góc B = 180^o – 71^o -38^o  = 71^o

Ta có: Góc B = góc M (=71^o ) =>ΔCBM cân tại C

Bài 2: Cho hình 16, biết ED = EF; EI là tia phân giác của góc DEF.

Chứng minh rằng:

a) ΔEID = ΔEIF.

b) ΔDIFcân.

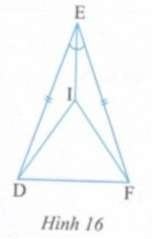
Giải:

a) Xét tam giác EID và EIF ta có:

+ ED = EF (gt)

+ Góc IED= Góc EIF (EI là tia phân giác của góc DEF)

+ EI là cạnh chung.

→ Do đó: ΔEID =ΔEIF(c.g.c)

b) ΔEID =ΔEIF (chứng minh câu a) => ID = IF. Do đó: tam giác DIF cân tại I.

Xem thêm Phiếu bài tập định lí Pitago