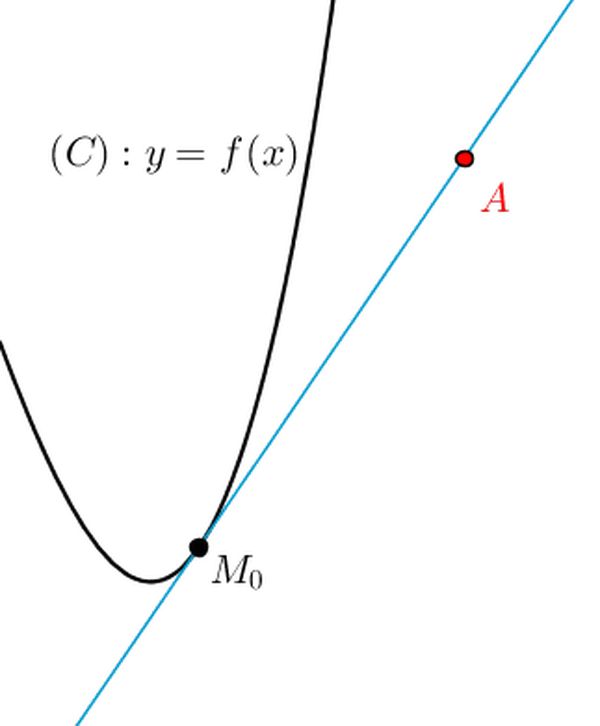
Các dạng toán Viết phương trình tiếp tuyến tại 1 điểm của đồ thị hàm số lớp 11

Đăng ngày bởi VanLoan | 1399 Views

Xem nhiều tuần qua:

Viết phương trình tiếp tuyến tại 1 điểm của đồ thị hàm số lớp 11.

Viết phương trình tiếp tuyến tại 1 điểm
Viết phương trình tiếp tuyến tại 1 điểm

 

Ý nghĩa hình học của đạo hàm

Đạo hàm của hàm số y= f(x) tại điểm \[{x_0}\] là hệ số góc của tiếp tuyến với đồ thị (C) của hàm số tại điểm \[M\left( {{x_0};{y_0}} \right)\]
 
Khi đó phương trình tiếp tuyến của (C) tại điểm M là:
 
\[y – {y_0} = f’\left( {{x_0}} \right)\left( {x – {x_0}} \right)\]

Các dạng Viết phương trình tiếp tuyến tại 1 điểm

Bài toán 1. Viết phương trình tiếp tuyến của đồ thị hàm số y= f(x) tại điểm \[M\left( {{x_0};{y_0}} \right)\]

– Tính đạo hàm của hàm số y= f(x)
 
– Tính \[f’\left( {{x_0}} \right)\]
 
-Tiếp tuyến của đồ thị hàm số y= f(x) tại \[M\left( {{x_0};{y_0}} \right)\] là:
 
\[y – {y_0} = f’\left( {{x_0}} \right)\left( {x – {x_0}} \right)\]
 

Bài toán 2. Viết phương trình tiếp tuyến của đồ thị hàm số y= f(x) biết hoành độ tiếp điểm \[x = {x_0}\].

+ Tính \[{y_0} = f\left( {{x_0}} \right)\].
 
+ Tính đạo hàm của hàm số y= f(x)
 
+ Tính \[f’\left( {{x_0}} \right)\]
 
⇒ phương trình tiếp tuyến: \[y – {y_0} = f’\left( {{x_0}} \right)\left( {x – {x_0}} \right)\]
 
 

Bài toán 3. Viết phương trình tiếp tuyến của đồ thị hàm số y= f(x) biết tung độ tiếp điểm bằng \[{y_0}\].

+ Gọi \[M\left( {{x_0};{y_0}} \right)\] là tiếp điểm
 
+ Giải phương trình \[f\left( x \right) = {y_0}\] ta tìm được các nghiệm \[{x_0}\].
 
+ Tính đạo hàm của hàm số ⇒ \[f’\left( {{x_0}} \right)\]
 
⇒ Phương trình tiếp tuyến của đồ thị hàm số : \[y – {y_0} = f’\left( {{x_0}} \right)\left( {x – {x_0}} \right)\]

Ví dụ minh họa

Ví dụ 1. Cho hàm số \[y = {x^3} – 2x + 1\]. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M( 0;1 )
 
A. y= 2x+ 3         B. y= -2x + 1         C.y= 4x+1         D. y= – 4x+1
 
Giải:
+ Đạo hàm của hàm số đã cho là: \[y’ = 3{x^2} – 2\]
 
⇒ \[y’\left( 0 \right) = – 2\]
 
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm M( 0;1) là:
 
\[\begin{array}{l}
y – 1 = – 2\left( {x – 0} \right)\\
\Leftrightarrow y = – 2x + 1
\end{array}\]
 
Ví dụ 2. Cho hàm số \[y = {x^2} + 2x – 6\]. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là 1?
 
A. y= 2x+1         B. y= – 6x+ 1         C. y= 4x- 7         D. y= -3x
 
Giải:
 
+ Ta có: y(1) = 12+ 2.1 – 6= -3 => Tọa độ tiếp điểm là (1; -3)
 
+ Đạo hàm của hàm số đã cho là: \[y’ = 2x + 2\]
 
⇒ y’(1) = 2.1+ 2= 4
 
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x= 1 là:
 
\[\begin{array}{l}
y + 3 = 4\left( {x – 1} \right)\\
\Leftrightarrow y = 4x – 7
\end{array}\]
 
Chọn C.
 
Ví dụ 3. Cho hàm số \[y = {x^3} + 4x + 2\]. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ là 2?
 
A. y= 4x+ 2         B. y = – 2x+ 1         C. y= 3x+ 1         D. y= 6x+ 1
 
Giải:
 
+ Xét phương trình:\[\begin{array}{l}
{x^3} + 4x + 2 = 2\\
\Leftrightarrow {x^3} + 4x = 0\\
\Leftrightarrow x = 0
\end{array}\]
Tọa độ tiếp điểm là (0;2)
 
+ Đạo hàm của hàm số đã cho là: \[y’ = 3{x^2} + 4\]
 
⇒ y’( 0) = 4
 
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ là 2:
 
\[\begin{array}{l}
y – 2 = 4\left( {x – 0} \right)\\
\Leftrightarrow y = 4x + 2
\end{array}\]
 
Chọn A.
 
Ví dụ 4. Cho hàm số \[y = – {x^3} + 2{x^2} + 2x + 1\] có đồ thị (C). Gọi A là giao điểm của đồ thị (C) với trục tung. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm A?
 
A. y= – 2x+ 1         B. y= 3x- 2         C. y= 4x+ 1         D. y= 2x+ 1
 
Giải:
 
+ Do A là giao điểm của đồ thị (C) với trục tung nên tọa độ điểm A( 0; 1) .
 
+ Đạo hàm \[y’ = – 3{x^2} + 4x + 2\]
 
⇒ y’( 0) = 2
 
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm A là:
 
\[\begin{array}{l}
y – 1 = 2\left( {x – 0} \right)\\
\Leftrightarrow y = 2x + 1
\end{array}\]
 
chọn D.
 
Ví dụ 5. Cho hàm số \[y = {x^2} – 3x + 2\]. Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại giao điểm của đồ thị hàm số với trục hoành ?
 
A. y= -x+ 1 và y= x – 2          B. y= x+ 1 và y= – x+ 3
 
C. y= – 2x + 1 và y= x- 2         D. Đáp án khác
 
Giải:
 
+ Giao điểm của đồ thị hàm số đã cho với trục hoành là nghiệm phương trình :
\[{x^2} – 3x + 2 = 0\]
 
Vậy đồ thị của hàm số đã cho cắt trục hoành tại hai điểm là A( 1; 0) và B( 2; 0).
 
+ Đạo hàm của hàm số đã cho: y’= 2x- 3
 
+ Tại điểm A( 1; 0) ta có: y’( 1)= – 1
 
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại A là:
 
\[\begin{array}{l}
y – 0 = – \left( {x – 1} \right)\\
\Leftrightarrow y = – x + 1
\end{array}\]
 
+ tại điểm B( 2; 0) ta có y’( 2)= 1
 
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại B là :
 
\[\begin{array}{l}
y – 0 = x – 2\\
\Leftrightarrow y = x – 2
\end{array}\]
 
Vậy có hai tiếp tuyến thỏa mãn là: y= -x+ 1 và y= x- 2
 
Chọn A.
 
Ví dụ 6. Cho hai đường thẳng \[{d_1}:2x + y – 3 = 0\] và \[{d_2}:x + y – 2 = 0\]. Gọi A là giao điểm của hai đường thẳng đã cho. Cho hàm số \[y = {x^2} + 4x + 1\] có đồ thị (C) . Viết phương trình tiếp tuyến của đồ thị (C) tại điểm A.
 
A. y= 3x- 5         B.y= 6x+ 1         C. y= 6x – 5         D. y= 2x+ 1
 
Giải: 
 
+ Giao điểm của hai đường thẳng d1 và d2 là nghiệm hệ phương trình:
 
\[\left\{ \begin{array}{l}
2x + y – 3 = 0\\
x + y – 2 = 0
\end{array} \right.\]
 
Vậy hai đường thẳng đã cho cắt nhau tại A( 1; 1).
 
+ Đạo hàm của hàm số đã cho là: y’= 2x+ 4
 
⇒ y’( 1) = 6.
 
⇒ Phương trình tiếp tuyến của đồ thị ( C) tại điểm A( 1; 1) là:
 
\[\begin{array}{l}
y – 1 = 6\left( {x – 1} \right)\\
\Leftrightarrow y = 6x – 5
\end{array}\]
 
Chọn C.
 
Ví dụ 7: Cho hàm số \[y = \frac{{2x + m + 1}}{{x – 1}}\] (C). Tìm m để tiếp tuyến của (C) tại điểm có hoành độ \[{x_0} = 0\] đi qua A(4; 3)
Giải: 
Giải:
 

Bài tập Viết phương trình tiếp tuyến

 
Đáp án
 
 
Like share và ủng hộ chúng mình nhé: