Tính khoảng cách giữa 2 đường thẳng chéo nhau bằng quan hệ song song.
Định nghĩa và tính chất – khoảng cách giữa 2 đường thẳng lớp 11
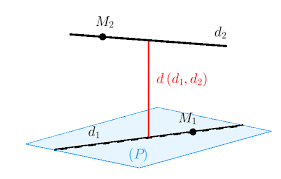
- Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó và mặt phẳng song song với nó mà chứa đường thẳng còn lại.
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
Khoảng cách giữa 2 đường thẳng trong hình chóp
Tính khoảng cách giữa 2 đường thẳng chéo nhau bằng cách dựng mặt song song
Có 2 phương pháp tính khoảng cách giữa hai đường thẳng chéo nhau
1. Cách 1: Tính độ dài đoạn vuông góc chung
Xem tại Kĩ thuật tính khoảng cách giữa hai đường thẳng chéo nhau lớp 11
2. Cách 2 Sử dụng mặt phẳng song song
Trong đề thi THPTQG, nội dung này ở mức điểm khá cao, rất hay thi vào cách làm thứ hai.
Phương pháp dựng mặt song song
Bước 1: Tìm một mặt phẳng (P) chứa b và (P) // a
Bước 2: Quy đổi khoảng cách
d(a;b) = d(a;(P)) = d(M;(P)) M nằm trên a
Bước 3: Đưa về khoảng cách từ điểm đến mặt phẳng
Ví dụ minh họa
Ví dụ 1: Cho chóp S.ABCD có SA vuông với đáy, ABCD là hình vuông cạnh a; Góc giữa SB và đáy là 60 độ
a) Tính d(SD; BC)
b) Tính d(AB, SC)
Giải:
a) Tính d(SD; BC)
Đường BC nằm dưới đáy, tìm mặt phẳng chứa SD và song song với BC; đó là (SAD) vì AD//BC
Khi đó d(BC;SD) = d(BC;(SAD)) = d(B;(SAD))
Ta được dạng tính khoảng cách từ điểm thuộc đáy đến mặt chứa đường cao
+ Từ B có BA vuông với AD => BA vuông với (SAD)
+ Vậy d(B;(SAD)) = AB = a
b) Tính d(AB; SC)
+ Đường AB nằm dưới đáy rồi nên cần tìm mặt chứa SC và song song với AB
+ Ta thấy CD//AB => (SCD)//AB
+ Ta có d(AB;SC) = d(AB;(SCD)) = d(A;(SCD))
Đây là dạng tính khoảng cách từ chân đường vuông góc đến mặt bên.
+ Từ chân vuông góc A, có AD vuông với giao tuyến CD; Kẻ tiếp AH vuông với SD
Ta được d(A;(SCD)) = AH
+ Tính AH:
\[\begin{array}{l}
\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}}\\
SA = AB.\tan {60^0} = a\sqrt 3 \\
\Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}} = \frac{4}{{3{a^2}}}\\
\Rightarrow AH = \frac{{a\sqrt 3 }}{2}
\end{array}\]
\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}}\\
SA = AB.\tan {60^0} = a\sqrt 3 \\
\Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}} = \frac{4}{{3{a^2}}}\\
\Rightarrow AH = \frac{{a\sqrt 3 }}{2}
\end{array}\]
Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh A, SA vuông góc với đáy. Góc giữa SC và đáy bằng 45 độ.
Tính d(AC;SB)
Tính d(AC;SB)
Giải:
+ AC nằm dưới đáy nên cần tìm mặt phẳng chứa SB và song song với AC
Không nhìn thấy mặt nào như vậy cả, cũng không thể dựng mặt vuông góc vì những mặt chứa đường cao thì hoàn toàn không vuông với AC.
+ Qua B (dưới đáy) kẻ đường thẳng song song với AC, cắt DA tại K ta được (SBK)//AC.
+ d(AC;SB) = d(AC;(SBK)) = d(A;(SBK))
+ Dựng d(A;(SBK)) như sau:
– Kẻ AM vuông với KB (thì M là trung điểm của KB)
– Nối SM
– Kẻ AH vuông với SM
ta được d(A;(SBK)) = AH
+ Tính AH:
\[\begin{array}{l}
\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{M^2}}}\\
*{\rm{ }}SA = AC.\tan {45^0} = a\sqrt 2 \\
*{\rm{ }}\frac{1}{{A{M^2}}} = \frac{1}{{A{K^2}}} + \frac{1}{{A{B^2}}}\\
{\rm{ = }}\frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} = \frac{2}{{{a^2}}}\\
\Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{2{a^2}}} + \frac{2}{{{a^2}}} = \frac{5}{{2{a^2}}}\\
\Rightarrow AH = \frac{{a\sqrt 2 }}{{\sqrt 5 }}
\end{array}\]
\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{M^2}}}\\
*{\rm{ }}SA = AC.\tan {45^0} = a\sqrt 2 \\
*{\rm{ }}\frac{1}{{A{M^2}}} = \frac{1}{{A{K^2}}} + \frac{1}{{A{B^2}}}\\
{\rm{ = }}\frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} = \frac{2}{{{a^2}}}\\
\Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{2{a^2}}} + \frac{2}{{{a^2}}} = \frac{5}{{2{a^2}}}\\
\Rightarrow AH = \frac{{a\sqrt 2 }}{{\sqrt 5 }}
\end{array}\]
Ví dụ 3: Cho hình chóp S.ABC có (SAB) và (SBC) cùng vuông góc với đáy; SB = AB = a; \[AC = a\sqrt 3 \]; tam giác ABC vuông tại A.
Tính d(BC;SA)
Tính d(BC;SA)
Giải:
+ BC nằm ở mặt đáy, cần tìm mặt chứa SA và song song với BC, cần vẽ thêm hình để dựng mặt phẳng.
+ Từ A dưới đáy kẻ AK//BC và AK = BC
Ta được (SAK) chứa SA và (SAK)//BC
+ d(BC;SA) = d(BC;(SAK)) = d(B;(SAK))
Đây là khoảng cách từ chân đường cao đến mặt bên
– Kẻ BM vuông với AK
– Nối SM, kẻ BH vuông với SM ta được d(B;(SAK)) = BH
+ Tính BH:
+ Từ A dưới đáy kẻ AK//BC và AK = BC
Ta được (SAK) chứa SA và (SAK)//BC
+ d(BC;SA) = d(BC;(SAK)) = d(B;(SAK))
Đây là khoảng cách từ chân đường cao đến mặt bên
– Kẻ BM vuông với AK
– Nối SM, kẻ BH vuông với SM ta được d(B;(SAK)) = BH
+ Tính BH:
\[\begin{array}{l}
\frac{1}{{B{H^2}}} = \frac{1}{{B{M^2}}} + \frac{1}{{S{A^2}}}\\
*{\rm{ }}\frac{1}{{B{M^2}}} = \frac{1}{{B{K^2}}} + \frac{1}{{B{A^2}}}\\
\Rightarrow \frac{1}{{B{H^2}}} = \frac{1}{{B{K^2}}} + \frac{1}{{B{A^2}}} + \frac{1}{{S{A^2}}}\\
{\rm{ = }}\frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}}{\rm{ = }}\frac{7}{{3{a^2}}}\\
\Rightarrow BH = \frac{{a\sqrt 3 }}{7}
\end{array}\]
\frac{1}{{B{H^2}}} = \frac{1}{{B{M^2}}} + \frac{1}{{S{A^2}}}\\
*{\rm{ }}\frac{1}{{B{M^2}}} = \frac{1}{{B{K^2}}} + \frac{1}{{B{A^2}}}\\
\Rightarrow \frac{1}{{B{H^2}}} = \frac{1}{{B{K^2}}} + \frac{1}{{B{A^2}}} + \frac{1}{{S{A^2}}}\\
{\rm{ = }}\frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}}{\rm{ = }}\frac{7}{{3{a^2}}}\\
\Rightarrow BH = \frac{{a\sqrt 3 }}{7}
\end{array}\]
Bài tập khoảng cách giữa 2 đường thẳng lớp 11

Bài viết khác cùng mục: