Cách tính khoảng cách từ điểm đến mặt phẳng (11) thi THPT QG

Cách tính khoảng cách từ điểm đến mặt phẳng (11) thi THPT QG

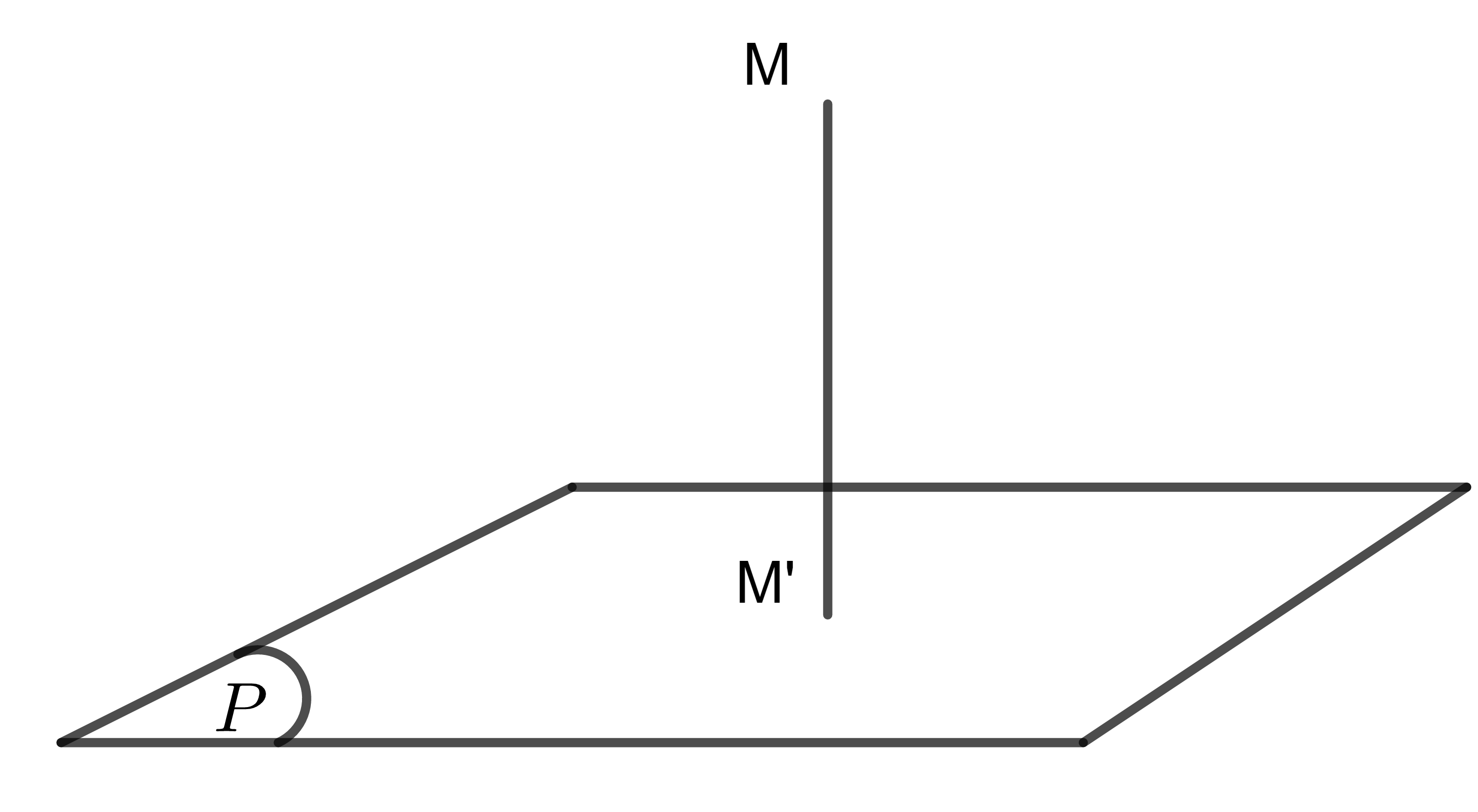
I. Định nghĩa – Khoảng cách từ điểm đến mặt phẳng lớp 11

Khoảng cách từ điểm M đến (P) là độ dài đoạn MH với H là hình chiếu vuông góc của M lên (P)

II. Khoảng cách từ điểm đến mặt phẳng hình không gian

Để dựng được khoảng cách từ điểm đến mặt phẳng cần xác định được vị trí chân đường vuông góc từ M xuống (P). Các bước là như sau:

+ Dựng một mặt phẳng (Q) chứa M và (Q) vuông góc với (P).

+ Từ M kẻ vuông góc vào giao tuyến của (P) và(Q), cắt giao tuyến tại H. Ta được H là hình chiếu của M.

III. Kĩ thuật tính khoảng cách từ điểm đến mặt phẳng

+ Nếu đường thẳng d //(P) thì khoảng cách từ mọi điểm trên d đến (P) là bằng nhau.

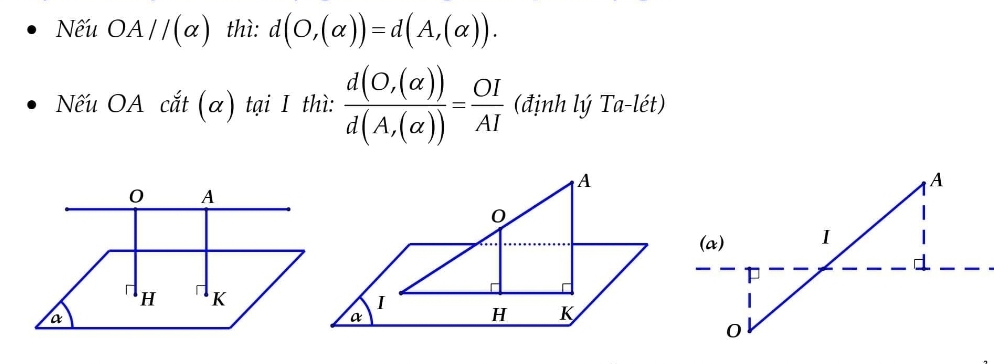
IV.  Tính khoảng cách từ điểm đến mặt phẳng trong hình chóp

Phân loại các dạng toán theo mặt phẳng cần tính khoảng cách

Tính khoảng cách từ ĐỈNH đến Mặt đáy

1. Từ đỉnh đến đáy: Là độ dài đường cao của chóp

2. Từ điểm bất kì đến đáy: Sử dụng công thức chuyển khoảng cách

Tính khoảng cách từ điểm trên đáy đến Mặt chứa đường cao

1. Từ điểm M thuộc đáy đến mặt chứa đường cao SA

Phương pháp: kẻ 1 đường vuông góc (màu xanh)

B1: Xác định giao tuyến của mặt chứa đường cao với đáy là AN.

B2: Kẻ 1 đường vuông góc MH từ điểm M đến giao tuyến AN, MH chính là khoảng cách cần tìm.

2. Từ điểm bất kì đến mặt chứa đường cao

Dùng công thức chuyển khoảng cách, đưa về khoảng cách từ điểm thuộc đáy đến mặt chứa đường cao

Ví dụ: Cho hình chóp S.ABC có đáy ABC có \[{\rm{AB}} = 3a;{\rm{ BC}} = 2a;{\rm{ }}\widehat {ABC} = {60^0}\] và \[SA \bot (ABC)\]

a) Tính khoảng cách từ C đến (SAB)

b) Gọi M là trung điểm của SC. Tính khoảng cách từ M đến (SAB)

c) Gọi G là trọng tâm tam giác SBC. Tính khoảng cách từ G đến (SAB).

Giải 

a) Mặt (SAB) chứa đường cao SA, cắt mặt đáy theo giao tuyến AB

Điểm C thuộc đáy, từ C kẻ CH vuông góc với AB, ta được CH là khoảng cách từ C đến (SAB).

\[\begin{array}{l}
CH = CB.\sin \widehat {ABH}\\
= 2a.\sin {60^0} = a\sqrt 3
\end{array}\]

b) Chuyển khoảng cách từ M đến (SAB) như sau:

M thuộc SC; SC cắt (SAB) tại S nên 

\[\begin{array}{l}
\frac{{d\left( {M;(SAB)} \right)}}{{d\left( {C;(SAB} \right)}} = \frac{{SM}}{{SC}} = \frac{1}{2}\\
\Rightarrow d\left( {M;(SAB)} \right) = \frac{{d\left( {C;(SAB} \right)}}{2} = \frac{{a\sqrt 3 }}{2}
\end{array}\]

c) Chuyển khoảng cách từ G đến (SAB) như sau:

G thuộc trung tuyến CN; CN cắt (SAB) tại N nên

\[\begin{array}{l}
\frac{{d\left( {N;(SAB)} \right)}}{{d\left( {C;(SAB} \right)}} = \frac{{NG}}{{NC}} = \frac{1}{3}\\
\Rightarrow d\left( {M;(SAB)} \right) = \frac{{d\left( {C;(SAB} \right)}}{3} = \frac{{a\sqrt 3 }}{3}
\end{array}\]

Tính khoảng cách từ chân đường cao đến Mặt bên

1. Từ chân đường cao H đến mặt bên: Kẻ 2 đường vuông góc

B1: Từ chân đường cao H kẻ 1 đường vuông góc với giao tuyến của mặt bên và đáy tại M

B2: Nối S với M rồi kẻ 1 đường vuông góc từ H đến SM, đây là khoảng cách cần tìm.

2. Từ điểm bất kì đến mặt bên

Sử dụng công thức chuyển khoảng cách, đưa về tính từ điểm thuộc đáy.

Ví dụ: Cho hình chóp đều S.ABCD cạnh đáy bằng a, chiều cao \[a\sqrt 2 \]

a) Tính khoảng cách từ tâm O của đáy đến (SCD)

b) Gọi N là trung điểm của BC, tính khoảng cách từ N đến (SCD)

c) Tính khoảng cách từ trung điểm I của SB đến (SCD).

d) Tính khoảng cách từ trung điểm J của SN đến (SCD)

Giải:

a) O là chân đường cao của chóp, (SCD) là mặt bên (cần kẻ 2 đường vuông góc màu xanh)

+ (SCD) cắt (ABCD) theo giao tuyến CD

+ Kẻ đường vuông góc OK vào giao tuyến CD

+ Nối SK, Kẻ tiếp đường vuông góc OH và SK, ta được OH là d(O;(SCD)) (học sinh tự chứng minh OH vuông với (SCD))

+ Tính OH: 

\[\begin{array}{l}
\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{K^2}}}\\
= \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {\frac{a}{2}} \right)}^2}}} = \frac{9}{{2{a^2}}}\\
\Rightarrow OH = \frac{{a\sqrt 2 }}{3}
\end{array}\]

b) Chuyển khoảng cách từ N đến (SCD) như sau:

ON//CD => ON // (SCD)

\[ \Rightarrow d\left( {N;(SCD)} \right) = d\left( {O;(SCD)} \right) = \frac{{a\sqrt 2 }}{3}\]

c) Chuyển khoảng cách từ I đến (SDC) như sau:

+ I thuộc SB; SB cắt (SCD) tại S nên

\[\begin{array}{l}
\frac{{d\left( {I;(SCD)} \right)}}{{d\left( {B;(SCD)} \right)}} = \frac{{SI}}{{SB}} = \frac{1}{2}\\
\Rightarrow d\left( {I;(SCD)} \right) = \frac{{d\left( {B;(SCD)} \right)}}{2}
\end{array}\]

Lại có B thuộc DO; DO cắt (SDC) tại O nên

\[\begin{array}{l}
\frac{{d\left( {B;(SCD)} \right)}}{{d\left( {O;(SCD)} \right)}} = \frac{{DO}}{{DB}} = \frac{1}{2}\\
\Rightarrow d\left( {B;(SCD)} \right) = 2d\left( {O;(SCD)} \right)
\end{array}\]

Vậy \[d\left( {I;(SCD)} \right) = \frac{{2d\left( {O;(SCD)} \right)}}{2} = d\left( {O;(SCD)} \right)\]

Hoặc cách như sau: IO là đường trung bình của tam giác SBD nên IO // SD => IO // (SCD)

=> \[d\left( {I;(SCD)} \right) = d\left( {O;(SCD)} \right)\]

d) Tính khoảng cách từ J thì chuyển qua N.