4 Bước cực dễ tìm Góc giữa mặt bên và mặt đáy hình chóp. Định nghĩa và cách xác định góc giữa 2 mặt phẳng – ví dụ minh họa. Giới thệu ến các em 4 bước cơ bản xác định góc giữa mặt bên và mặt đáy cực nhanh và chính xác.
Định nghĩa góc giữa 2 mặt phẳng – Góc giữa 2 mặt phẳng lớp 11
Để giúp các bạn nắm vững kiến thức về góc giữa 2 mặt phẳng, đầu tiên chúng ta sẽ tìm hiểu về khái niệm của góc giữa 2 mặt phẳng.
Khái niệm: Góc giữa 2 mặt phẳng là gì? Góc giữa 2 mặt phẳng là góc được tạo bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Trong không gian 3 chiều, góc giữa 2 mặt phẳng còn được gọi là ‘góc khối’, là phần không gian bị giới hạn bởi 2 mặt phẳng. Góc giữa 2 mặt phẳng được đo bằng góc giữa 2 đường thẳng trên mặt 2 phẳng có cùng trực giao với giao tuyến của 2 mặt phẳng.
Tính chất: Từ định nghĩa trên ta có:
- Góc giữa 2 mặt phẳng song song bằng 0 độ,
- Góc giữa 2 mặt phẳng trùng nhau bằng 0 độ.
Tính góc giữa 2 mặt phẳng trong không gian – Góc giữa mặt bên và mặt đáy
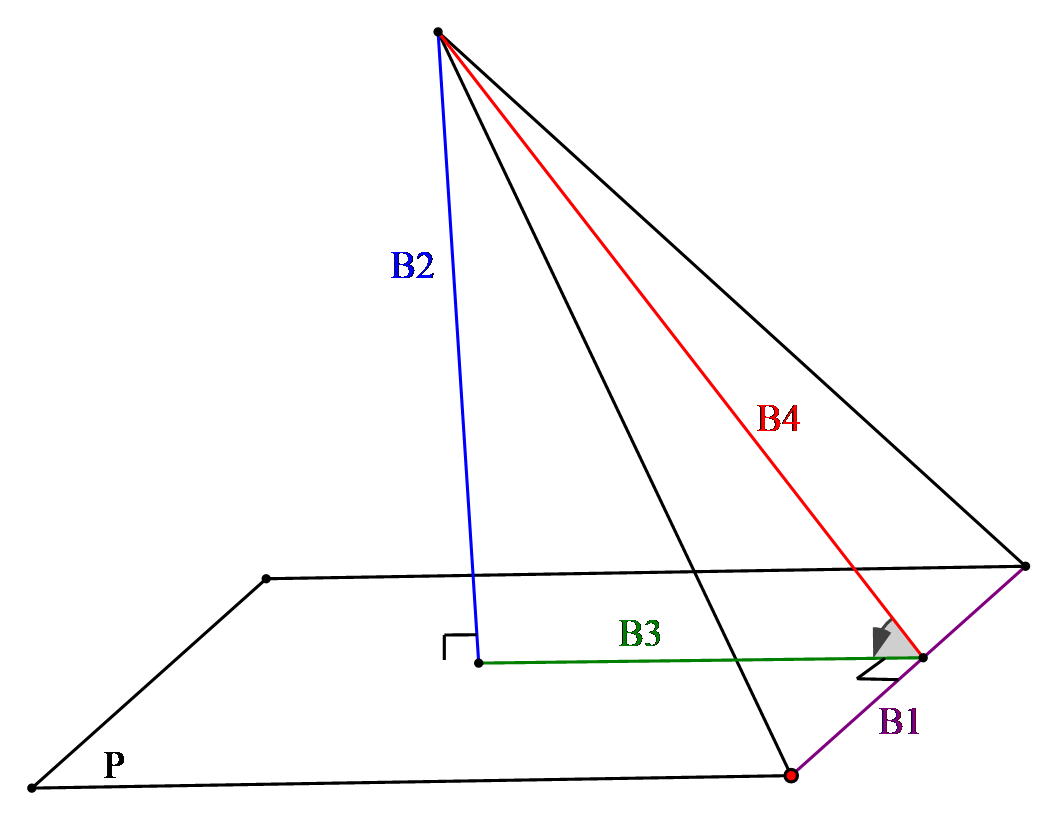
Bước 3: Tiếp tục hạ vuông góc với giao tuyến
Bước 4: Nối lên điểm còn lại ở B2. Đỉnh góc nằm trên giao tuyến
Ví dụ minh họa – Xác định góc giữa mặt bên và mặt đáy
Ví dụ 1: – Cách vẽ góc giữa mặt bên và đáy
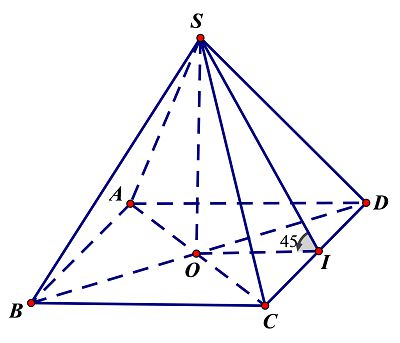
Cho hình chóp S.ABCD có SA vuông góc với đáy, ABCD là hình chữ nhật AB=a; AD=2a; SA=2a.
\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{2a}}{a} = 2\\
\Rightarrow \widehat {SBA} \approx {63^0}
\end{array}\]
\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}}\\
{\rm{ = }}\frac{1}{{{a^2}}} + \frac{1}{{4{a^2}}} = \frac{5}{{4{a^2}}}\\
\Rightarrow AH = \frac{{2a}}{{\sqrt 5 }}
\end{array}\]
\tan \widehat {SHA} = \frac{{SA}}{{AH}} = \frac{{2a}}{{\frac{{2a}}{{\sqrt 5 }}}} = \sqrt 5 \\
\Rightarrow \widehat {SHA} \approx {66^0}
\end{array}\]
Tính góc giữa (SBC) và (ABC)
+ Giao tuyến BC
+ Từ S kẻ vuông góc xuống đáy (ABC) ta được điểm A
+ Từ A kẻ vuông góc vào BC ta được điểm M (M là trung điểm của BC)
+ Nối M lên S ta được góc SMA
+ Tính:
– Tam giác SAM vuông tại A nên: \[\tan \widehat {SMA} = \frac{{SA}}{{AM}}\] Với \[AM = \frac{{a\sqrt 3 }}{2}\] (đường cao của tam giác đều)
\tan \widehat {SMA} = \frac{{SA}}{{AM}} = \frac{{\frac{{3a}}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \sqrt 3 \\
\Rightarrow \widehat {SMA} = {60^0}
\end{array}\]
+ Giao tuyến BD
+ Từ điểm A’ kẻ vuông góc xuống đáy (ABCD) ta được điểm A
+ Từ A kẻ vuông góc vào giao tuyến ta được O (O là giao 2 đường chéo)
+ Nối O với A’ ta được góc A’OA
+ Tính
– Có \[AO = \frac{{a\sqrt 2 }}{2}\]
\tan \widehat {A’OA} = \frac{{A’A}}{{AO}} = \frac{a}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 2 \\
\Rightarrow \widehat {A’OA} \approx {55^0}
\end{array}\]
Tính góc giữa (SBC) và (ABC)
Giải:
+ Giao tuyến BC
Tính góc giữa (SBC) và mặt đáy.
AC = \sqrt {A{B^2} – B{C^2}} \\
{\rm{ = }}\sqrt {{a^2} – \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\\
\Rightarrow HM = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{4}
\end{array}\]
\tan \widehat {SMH} = \frac{{SH}}{{HM}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\frac{{a\sqrt 3 }}{4}}} = 2\\
\Rightarrow \widehat {SMH} \approx {63^0}
\end{array}\]
Kĩ thuật tính khoảng cách giữa hai đường thẳng chéo nhau
Cách xác định góc giữa đường thẳng và mặt phẳng lớp 11
Cách tính khoảng cách từ điểm đến mặt phẳng

Bài viết khác cùng mục: