Cách xác định góc giữa đường thẳng và mặt phẳng lớp 11. Các bước xác định góc giữa đường thẳng và mặt phẳng
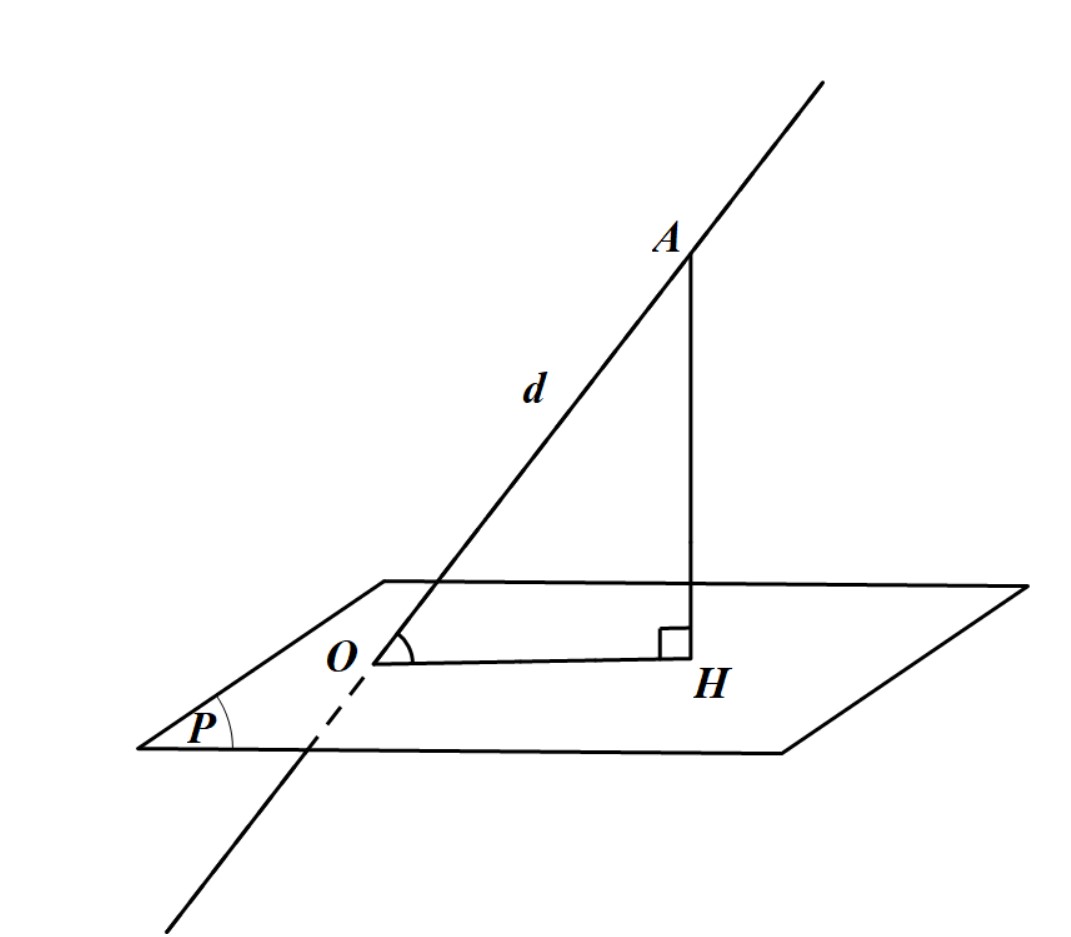
Các bước xác định góc giữa đường thẳng d và mặt phẳng (P)
Bước 1:Tìm điểm chung của d và (P)
Bước 2: Từ 1 điểm còn lại của d, hạ đường vuông góc xuống (P)
Bước 3: Nối chân vuông góc với điểm chung
Cách tính một góc
- Muốn tính một góc, xét tam giác cùng tên với góc đó
- Định lý Pi ta go
- Hệ thức lượng trong tam giác vuông
- Định lý Sin, cosin
Xác định góc giữa đường thẳng và mặt phẳng – Bài tập minh họa
Ví dụ 1: Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy. Tam giác ABC vuông tại B
a) Xác định góc giữa cạnh SB với (ABC)
b) Xác định góc giữa cạnh SC với (ABC)
c) Xác định góc giữa cạnh SC vứi (SAB)
Giải:
![]()
a) Xác định góc giữa cạnh SB với (ABC)
+ \[SB \cap \left( {ABC} \right) = \left\{ B \right\}\]
+ Từ S hạ vuông góc xuống (ABC) ta được SA
+ Đưa điểm chung và giữa ta được \[\widehat {SBA}\]
b) Xác định góc giữa cạnh SC với (ABC)
+ \[SC \cap \left( {ABC} \right) = \left\{ C \right\}\]
+ Từ S hạ vuông góc xuống (ABC) ta được SA
+ Chèn điểm chung C vào ta được \[\widehat {SCA}\]
c) Xác định góc giữa cạnh SC với (SAB)
+ \[SC \cap \left( {SAB} \right) = S\]
+ Từ C kẻ vuông góc và (SAB) ta được CB (cần chứng minh CB vuông góc với (SAB))
+ Chen điểm chung S vào ta được \[\widehat {CSB}\]
Ví dụ 2: Cho hình chóp S.ABCD có SA vuông góc với đáy. Đáy ABCD là hình vuông tâm O.
a) Xác định góc giữa SO và (ABCD)
b) Xác định góc giữa SC và (SAD)
c) Xác định góc giữa SB và (SAC)
Giải:
![]()
a) Xác định góc giữa SO và (ABCD)
+ \[SO \cap \left( {ABCD} \right) = \left\{ O \right\}\]
+ Từ S kẻ vuông góc vào (ABCD) ta được SA
+ Chen điểm chung O vào giữa ta được \[\widehat {SOA}\]
b) Xác định góc giữa SC và (SAD)
+ \[SC \cap \left( {SAD} \right) = S\]
+ Từ C kẻ vuông góc vào (SAD) ta được CD ( cần chứng minh \[CD \bot \left( {SAD} \right)\])
+ Chèn điểm chung S vào giữa ta được \[\widehat {CSD}\].
c) Xác định góc giữa SB và (SAC)
+ \[SB \cap \left( {SAC} \right) = S\]
+ Từ B hạ vuông góc và (SAC) ta được BO ( cần chứng minh \[BO \bot \left( {SAC} \right)\])
+ Chen điểm chung S và giữa ta được \[\widehat {BSO}\].
Ví dụ 3: Cho hình chóp S.ABCD có SA vuông góc với đáy. Biết đáy là hình vuông cạnh a, \[SA = a\sqrt 3 \]. Tính góc giữa đường thẳng AC và mặt phẳng (SBC).
Giải:
![]()
+ \[AC \cap \left( {SBC} \right) = C\]
+ Kẻ \[AH \bot SB\]
\[\begin{array}{l}
\Rightarrow \left\{ \begin{array}{l}
AH \bot BC{\rm{ }}\left( {BC \bot \left( {SAB} \right)} \right)\\
AH \bot SB
\end{array} \right.\\
\Rightarrow AH \bot \left( {SBC} \right)
\end{array}\]
+ Chen điểm chung vào giữa ta được \[\widehat {ACH}\]
+ Xét tam giác SAB vuông tại A ta có
\[\begin{array}{l}
\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}}\\
{\rm{ = }}\frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}} = \frac{4}{{3{a^2}}}\\
\Rightarrow AH = \frac{{a\sqrt 3 }}{2}\\
\sin C = \frac{{AH}}{{AC}} = \frac{{a\sqrt 3 }}{2}:a\sqrt 2 = \frac{{\sqrt 3 }}{{2\sqrt 2 }}\\
\Rightarrow C \approx {38^0}
\end{array}\]
Ví dụ 4: Cho hình lập phương ABCD.A’B’C’D’ cạnh a
a) Tính góc giữa B’D và (AA’D’D)
b) Tính góc giữa BD và mặt phẳng (B’AC)
Giải:
![]()
a)Tính góc giữa B’D và (AA’D’D)
+ \[B’D \cap \left( {AA’DD} \right) = D\]
+ Từ B’ hạ vuông góc với (AA’D’D) ta được B’A’ (tự chứng minh \[B’A’ \bot \left( {AA’D’D} \right)\])
+ Chen điêểm chung vào giữa ta được \[\widehat {B’DA’}\]
+ Tính :
\[\begin{array}{l}
\tan \widehat {B’DA’} = \frac{{B’A’}}{{DA’}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\\
\Rightarrow \widehat {B’DA’} \approx {35^0}
\end{array}\]
b) Tính góc giữa BD và mặt phẳng (B’AC)
![]()
+ \[BD \cap \left( {B’AC} \right) = O\]
+ Từ B kẻ vuông góc vào B’O ta được BH ( cần chứng minh \[BH \bot \left( {B’AC} \right)\])
(Đây cũng là cách dựng khoảng cách từ điểm B đến mặt phẳng (B’AC)
Học sinh xem chi tiết tại Cách tính khoảng cách từ điểm đến mặt phẳng )
+ Chen điểm chung vào ta được \[\widehat {BOH}\]
+ Tính:
\[\begin{array}{l}
\tan \widehat {B’OB} = \frac{{BB’}}{{BO}} = \frac{a}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 2 \\
\Rightarrow \widehat {B’OB} \approx {55^0}
\end{array}\]
Phiếu bài tập góc giữa đường thẳng và mặt phẳng

Bài viết khác cùng mục: