Bài tập góc có đỉnh nằm trong và ngoài đường tròn

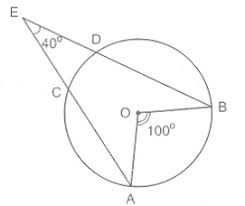
+ Định lí 1. Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

+ Định lí 2. Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

Dạng 1. Chứng minh hai góc hoặc hai đoạn thẳng bằng nhau.
Phương pháp giải: Sử dụng hai định lý về số đo của góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn.
Dạng 2. Chứng minh hai đường thẳng song song hoặc vuông góc. Chứng minh các đẳng thức cho trước.
Phương pháp giải: Áp dụng hai định lý về số đo của góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn để có được các góc bằng nhau, cạnh bằng nhau. Từ đó, ta suy điều cần chứng minh.