Phiếu bài tập Góc nội tiếp hình học lớp 9. Tổng hợp kiến thức lý thuyết, các dạng bài tập và phiếu bài tập tổng hợp về góc nội tiếp.
Kiến thức cần nhớ Góc nội tiếp
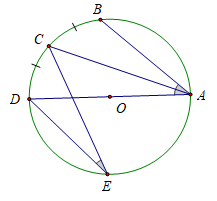
Góc BAC có đỉnh A nằm trên đường tròn và hai cạnh AB, AC là hai dây cung được gọi là góc nội tiếp. Cung BC nằm bên trong được gọi là cung bị chắn. sdBAC = 1/2.sdBC (số đo của góc nội tiếp bằng nửa số đo của cung bị chắn).
Tính chất: Trong một đường tròn:
+ Các góc nội tiếp bằng nhau thì chắn các cung bằng nhau.
+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+ Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
![]()
+ Điểm nằm chính giữa cung chia cung đó thành hai cung có số đo bằng nhau. Hai góc nội tiếp chắn hai cung đó thì bằng nhau.
+ Để chứng minh đẳng thức hình học, suy nghĩ quy về chứng minh tam giác đồng dạng dựa vào các góc nội tiếp cùng chắn một cung hoặc hai cung bằng nhau trong một đường tròn.
+ Góc nội tiếp (nhỏ hơn bằng 90 độ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Các dạng bài tập về góc nội tiếp
Dạng 1: Chứng minh các tam giác đồng dạng, hệ thức về cạnh, hai góc bằng nhau, các đoạn thẳng bằng nhau
Phương pháp:
Ta thường sử dụng hệ quả
Trong một đường tròn:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
c) Góc nội tiếp (nhỏ hơn hoặc bằng 90∘) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.
d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
Dạng 2: Tính độ dài, tính diện tích.
Dạng 3: Bài toán dựa vào hệ quả của góc nội tiếp chứng minh ba điểm thẳng hàng.
Dạng 4: Chứng minh hai đường thẳng vuông góc, song song. Tính độ dài, diện tích
Phương pháp:
Ta sử dụng hệ quả để suy ra các góc bằng nhau từ đó chứng minh theo yêu cầu bài toán.
![]()
Dạng 5: Nâng cao phát triển tư duy.
Phiếu bài tập Góc nội tiếp hình học lớp 9
Xem thêm Phiếu bài tập góc tạo bởi tiếp tuyến và dây cung

Bài viết khác cùng mục: