Giải Phương trình chứa căn lớp 9 – Ôn thi vào lớp 10 chuyên

Giải Phương trình chứa căn lớp 9 là một nội dung không thể thiếu trong các đề thi vào lớp 10 chuyên và chất lượng cao.

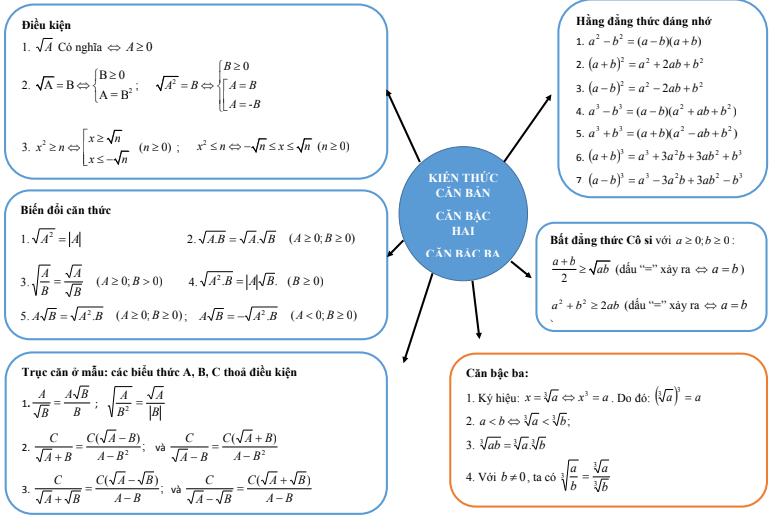
Giải Phương trình chứa căn lớp 9

Với nội dung rộng lớn, các bài tập có từ khó đến dễ, từ cơ bản đến phức tạp, phương trình vô tỷ luôn là một thử thách lớn với các bạn học sinh lớp 9.

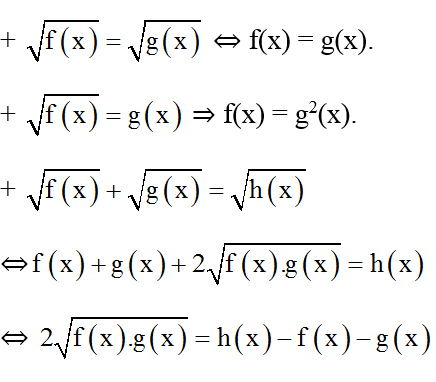
Phương trình vô tỉ ở lớp 9 là những phương trình có dấu căn, tuy nhiên, những phương trình này thường chứa dấu căn bậc hai hoặc căn bậc ba.

Chuyên đề hệ phương trình chứa căn

Trong chương trình môn toán ở các lớp THCS kiến thức về phương trình vô tỉ không nhiều song lại rất quan trọng đó là những tiền đề cơ bản để học sinh tiếp tục học lên ở THPT.
Khi giải toán về phương trình vô tỉ đòi hỏi học sinh nắm vững các kiến thức cơ bản về căn thức, phương trình, hệ phương trình, các phép biến đổi đại số…Học sinh biết vận dụng linh hoạt, sáng tạo các kiến thức, kỹ năng từ đơn giản đến phức tạp. “Một số phương pháp giải phương trình vô tỷ” giúp học sinh phát triển tư duy, phát huy tính tích cực chủ động, sáng tạo trong giải toán. Đồng thời giáo dục tư tưởng, ý thức, thái độ, lòng say mê học toán cho học sinh.

PHÂN DẠNG TOÁN CHỨA CĂN.

DẠNG 1: RÚT GỌN BIỂU THỨC CHỨA SỐ.
+ Loại 1: Dạng chứa căn số học đơn giản.
+ Loại 2: Dạng “biểu thức số trong căn” tiềm ẩn “là hằng đẳng thức”.
+ Loại 3: Dạng sử dụng biểu thức liên hợp, trục căn thức, quy đồng.
+ Loại 4: Chứng minh đẳng thức số.
+ Loại 5: Chứng minh bất đẳng thức.
+ Loại 6: Căn bậc ba.
DẠNG 2: CÁC DẠNG TOÁN CĂN CHỨA CHỮ (CHỨA ẨN).
DẠNG TOÁN GIẢI PHƯƠNG TRÌNH CHỨA CĂN THỨC.
+ Loại 1: Phương trình trong căn có thể viết dưới dạng bình phương của một biểu thức.
+ Loại 2: Phương trình dạng √f(x) = √g(x).
+ Loại 3: Phương trình chứa biểu thức dưới dấu căn không viết được dưới dạng bình phương (trong phương trình chỉ chứa một căn thức).
+ Loại 4: Phương trình chứa nhiều căn thức, các căn thức có thể đưa về dạng giống nhau.
[ads] + Loại 5: Phương trình chứa các căn khác nhau, biểu thức trong căn không viết được dưới dạng bình phương.
+ Loại 6: Quy về phương trình bậc hai bằng phương pháp đặt ẩn phụ.
+ Loại 7: Phương trình chứa căn mà biểu thức trong căn ở dạng thương hoặc dạng tích.
+ Loại 8: Giải các phương trình căn bậc ba.
DẠNG TOÁN RÚT GỌN BIỂU THỨC CHỨA CĂN.
+ Loại 1: Sử dụng các hằng đẳng thức.
+ Loại 2: Sử dụng phương pháp quy đồng.
+ Loại 3: Làm xuất hiện nhân tử chung rồi đơn giản biểu thức chứa căn sau đó quy đồng.
DẠNG TOÁN CHỨA CĂN VÀ BÀI TOÁN PHỤ.
+ Bài toán 1: Tìm ẩn để biểu thức thỏa mãn một điều kiện cho trước (lớn hơn, nhỏ hơn, bằng một giá trị cho trước).
+ Bài toán 2. Tính giá trị của biểu thức tại giá trị cho trước.
+ Bài toán 3: Tìm a nguyên để biểu thức nguyên.
+ Bài toán 4: Tìm giá trị lớn nhất, nhỏ nhất.
PHẦN BÀI TẬP.
BÀI TOÁN TỔNG HỢP – TỰ GIẢI.
PHẦN ĐÁP ÁN – HƯỚNG DẪN GIẢI.
DẠNG TOÁN RÚT GỌN BIỂU THỨC CHỨA SỐ.
+ Loại 1: Dạng chứa căn số học đơn giản.
+ Loại 2: Dạng “biểu thức số trong căn” tiềm ẩn “là hằng đẳng thức”.
+ Loại 3: Dạng sử dụng biểu thức liên hợp, trục căn thức, quy đồng.
DẠNG TOÁN RÚT GỌN BIỂU THỨC CHỨA CĂN.
+ Loại 1: Sử dụng các Hằng đẳng thức.
+ Loại 2: Sử dụng phương pháp quy đồng.
+ Loại 3: Làm xuất hiện nhân tử chung rồi đơn giản biểu thức chứa căn sau đó quy đồng.

Các bài tập giải phương trình chứa căn lớp 9

Phương trình vô tỉ lớp 9 bài tập

Phương trình vô tỉ là loại toán khó đối với học sinh THCS, nhiều học sinh không biết giải phương trình vô tỉ như thế nào, chưa nắm vững có những phương pháp nào. Các bài toán về phương trình vô tỉ là một dạng toán hay và khó, có nhiều trong các đề thi học sinh giỏi các cấp, thi vào lớp 10 THPT. Tuy nhiên, các tài liệu, các sách tham khảo, sách giáo viên cũng chưa có sách nào đề cập chi tiết cụ thể các phương pháp giải loại toán này. Có chăng chỉ là gợi ý chung, sơ lược và đưa ra lời giải các bài toán một cách rời rạc. Đặc biệt trong sách giáo khoa lớp 9 dạng bài
toán này cũng chưa được đưa vào phân phối chương trình mà chỉ lồng ghép ở phần bài tập trong chương I căn bậc hai, căn bậc ba. Đây là một vấn đề quan trọng và bức thiết. Lâu nay chúng ta đang tìm kiếm một phương pháp dạy học sinh giải dạng toán này sao cho đạt hiệu quả cao nhất.

Vì vậy việc nghiên cứu các phương pháp giải phương trình vô tỉ là rất thiết thực, giúp giáo viên nắm vững nội dung và xác định được phương pháp giảng dạy phần này đạt hiệu quả, góp phần nâng cao chất lượng dạy và học, dặc biệt là chất lượng học sinh giỏi và giáo viên giỏi ở các trường THCS.