Bài tập tính chất đường phân giác trong tam giác lớp 8 kèm đáp án chi tiết. Tính chất đường phân giác là một trong những định lý quan trọng trong chương trình toán phổ thông. Học sinh ngoài việc nhớ được định lý cần phải biết áp dụng linh hoạt vào các bài tập từ dễ đến khó. Để giúp các bạn học sinh nắm chắc định lý hơn, dưới đây là hệ thống các bài tập ứng dụng tính chất đường phân giác từ cơ bản đến nâng cao kèm theo lời giải chi tiết dễ hiểu.
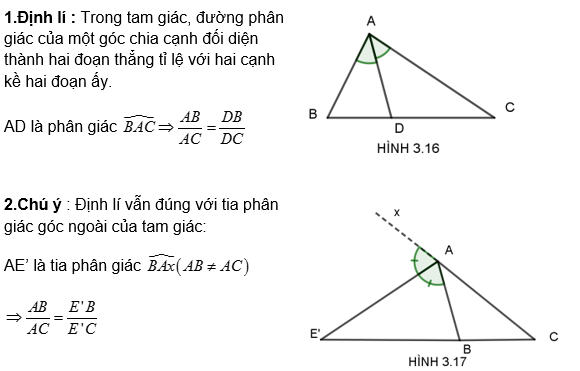
Đường phân giác của một góc là bài học quan trọng nằm trong chương trình toán 8 THCS. Vậy tia phân giác là gì? Tính chất đường phân giác trong tam giác như nào?… Có thể thấy, bên cạnh đường trung tuyến và trung trực thì đường phân giác cũng có những tính chất thú vị, đặc biệt là trong tam giác vuông. Vậy tính chất tia phân giác của một góc có gì đặc biệt? Đặc điểm của đường phân giác trong tam giác vuông như nào?… Cùng theo dõi bài viết ngay dưới đây
Các dạng toán thường gặp
Dạng 1: Tính độ dài cạnh, chu vi, diện tích
Phương pháp:
Sử dụng tính chất đường phân giác của tam giác và tỉ lệ thức để biến đổi và tính toán.
+ Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Dạng 2: Chứng minh đẳng thức hình học và các bài toán khác
Phương pháp:
Sử dụng tính chất đường phân giác của tam giác: “Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.”
Bài tập tính chất đường phân giác
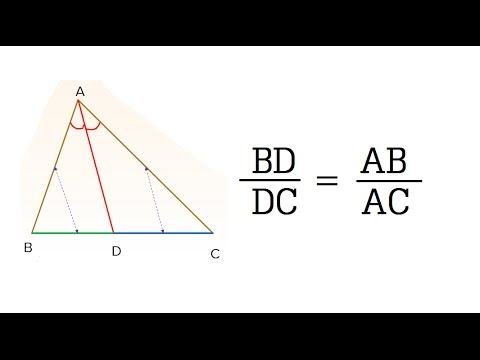
Download Bài tập tính chất đường phân giác lớp 8 đáp án chi tiết

Bài viết khác cùng mục: