Các dạng bài tập đường trung bình của tam giác có giải

Các dạng bài tập đường trung bình của tam giác có giải. Đường trung bình là một nội dung hết sức quan trọng trong chương trình hình học phổ thông. Các em sẽ dùng đến nó trong suốt những năm học tiếp theo này. Tài liệu gồm tóm tắt lý thuyết và hệ thống bài tập đa dạng từ cơ bản đến nâng cao, phần đáp án sẽ giúp các em đối chiếu bài làm của mình.

Với Các dạng bài tập về đường trung bình của tam giác, hình thang và cách giải môn Toán lớp 8 phần Hình học sẽ giúp học sinh nắm vững lý thuyết, biết cách làm các dạng bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 8.

I. Lí thuyết – Đường trung bình của tam giác

II. Dạng bài tập

Dạng 1. Sử dụng định nghĩa và định lý về đường trung bình của tam giác để chứng minh

 

Phương pháp giải: Sử dụng định nghĩa, định lý để suy ra điều cần chứng minh.

 

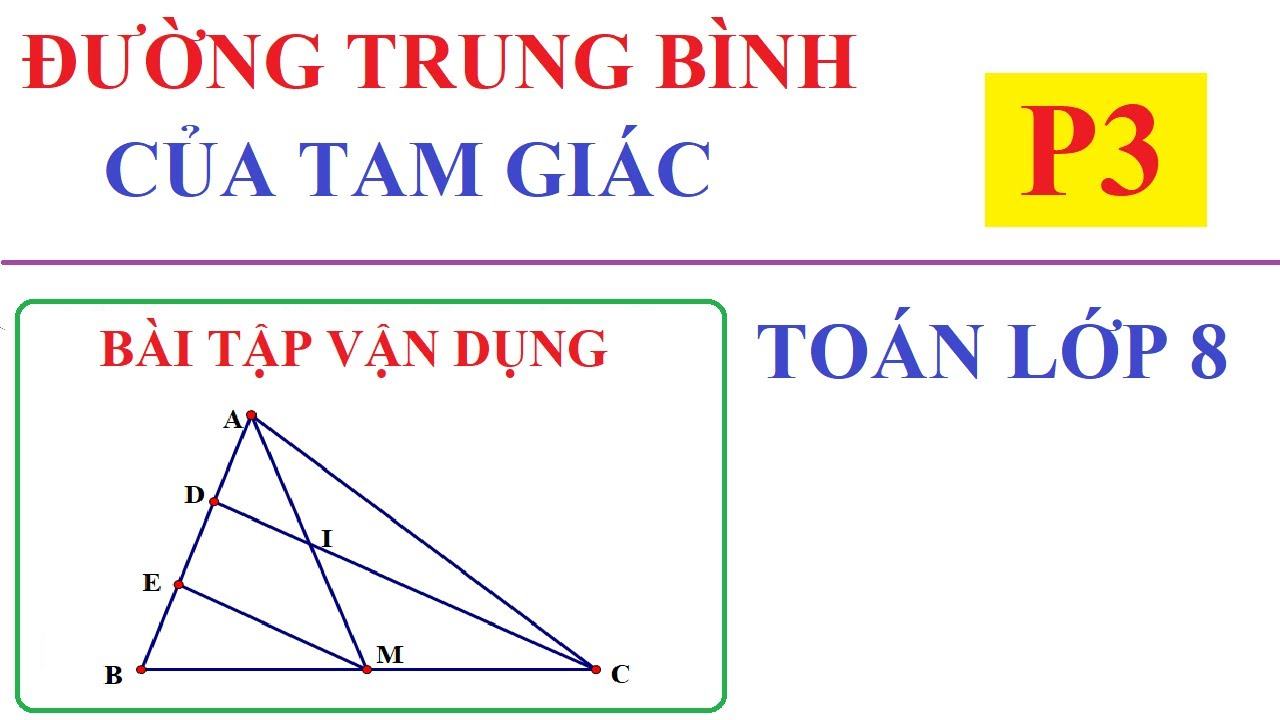
Ví dụ: Cho tam giác ABC, có AM là trung tuyến ứng với BC. Trên cạnh AB lấy điểm D và E sao cho AD = DE = EB. Đoạn CD cắt AM tại I. Chứng minh:

 

a) EM song song với DC;

 

b) I là trung điểm AM;

 

c) DC = 4DI.

 

Lời giải:

a) Vì ED = EB nên E là trung điểm của BD

 

Lại có M là trung điểm của BC 

 

Suy ra EM là đường trung bình của tam giác BCD

 

=> EM // CD

 

b) Xét tam giác AEM có:

 

 Ta có: AD = DE nên D là trung điểm AE.

 

Lại có I ∈ DC => DI // EM (do DC // EM)

 

Do đó: DI đi qua trung điểm AM

 

=> I là trung điểm của AM

 

c) Từ câu a ta có: EM là đường trung bình của tam giác BCD => EM = 1/2 DC

Lại có I là trung điểm của AM, D là trung điểm của AE 

 

=> DI là đường trung bình của tam giác AEM => DI = 1/2EM

Vậy DI = 1/2EM = 1/2.1/2DC = 1/4DC = 4DI

Dạng 2. Sử dụng định lý đường trung bình của hình thang để chứng minh

Phương pháp giải: Sử dụng định nghĩa và các định lý liên quan đến đường trung bình của hình thang để chứng minh.

Ví dụ: Cho hình thang ABCD (AB // CD). Các đường phân giác ngoài của Các dạng bài tập về đường trung bình của tam giác, hình thang và cách giải cắt nhau tại E, cắc đường phân giác ngoài Các dạng bài tập về đường trung bình của tam giác, hình thang và cách giải cắt nhau tại F. Chứng minh:

 

a) EF song song AB và CD.

 

b) EF có độ dạng bằng nửa chu vi hình thang ABCD.

 

Lời giải:

 

Dạng 3. Sử dụng phối hợp đường trung bình của tam giác và đường trung bình của hình thang để chứng minh.

Phương pháp giải: Sử dụng kết hợp các định nghĩa định lý về đường trung bình để chứng minh bài toán

 

Ví dụ: Cho hình thang ABCD (AB // CD, AB < CD) . Gọi M, N, P, Q lần lượt là trung điểm của AD, BD, AC, BC. Chứng minh:

 

a) M, N ,P, Q cùng nằm trên một đường thẳng

 

b) Các dạng bài tập về đường trung bình của tam giác, hình thang và cách giải 

 

Lời giải:

 

Các dạng bài tập về đường trung bình của tam giác, hình thang và cách giải

 

a) Ta có M là trung điểm của AD, Q là trung điểm BC

 

=> MQ là đường trung bình của hình thang ABCD

 

=> MQ // AB // CD (1)

 

M là trung điểm của AD, N là trung điểm của BD

 

=> MN là đường trung bình của tam giác DAB

 

=> MN // AB (2)

 

P là trung điểm của AC, Q là trung điểm của BC

 

=> PQ là đường trung bình của tam giác ABC

 

=> PQ // AB (3)

 

Từ (1), (2) , (3) => MN // MQ // QP // AB

 

=> bốn điểm M, N, P, Q thẳng hàng

 

=> M, N, P, Q thuộc cùng một đường thẳng

 

b) Đặt AB = a; CD = b

 

Vì MQ là đường trung bình của hình thang ABCD

\[ \Rightarrow MQ = \frac{{AB + CD}}{2} = \frac{{a + b}}{2}\]

Lại có MN, PQ lần lượt là đường trung bình của tam giác ABD và ABC

\[ \Rightarrow MN = \frac{a}{2};PQ = \frac{a}{2}\]

Ta có:

\[\begin{array}{l}
MQ = MN + NP + PQ = \frac{a}{2} + NP + \frac{a}{2} = \frac{{a + b}}{2}\\
\Rightarrow NP = \frac{{a + b}}{2} – \frac{a}{2} – \frac{a}{2}\\
\Rightarrow NP = \frac{{b – a}}{2} = \frac{1}{2}\left( {CD – AB} \right)
\end{array}\]

Bài tập đường trung bình của tam giác – Bài tập về đường trung bình có đáp án

Xem thêm Các dạng bài tập hình thang cân có lời giải chi tiết

Các dạng bài tập đối xứng trục lớp 8 có lời giải chi tiết;