160 câu trắc nghiệm hàm số lớp 12 có đáp án

Xem nhiều tuần qua:

160 câu trắc nghiệm hàm số lớp 12 có đáp án. Tài liệu gồm 160 câu được phân dạng và tuyển chọn các bài tập trắc nghiệm chuyên đề hàm số có đáp án trong chương trình Giải tích 12 chương 1, các bài tập chuyên đề hàm số với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng và vận dụng bậc cao, ngoài ra có các bài toán mở rộng và các bài toán để vận dụng kỹ năng giải toán bằng máy tính cầm tay Casio.

Nội dung chính:

Các dạng toán về xét tính đơn điệu của hàm số cơ bản đến nâng cao

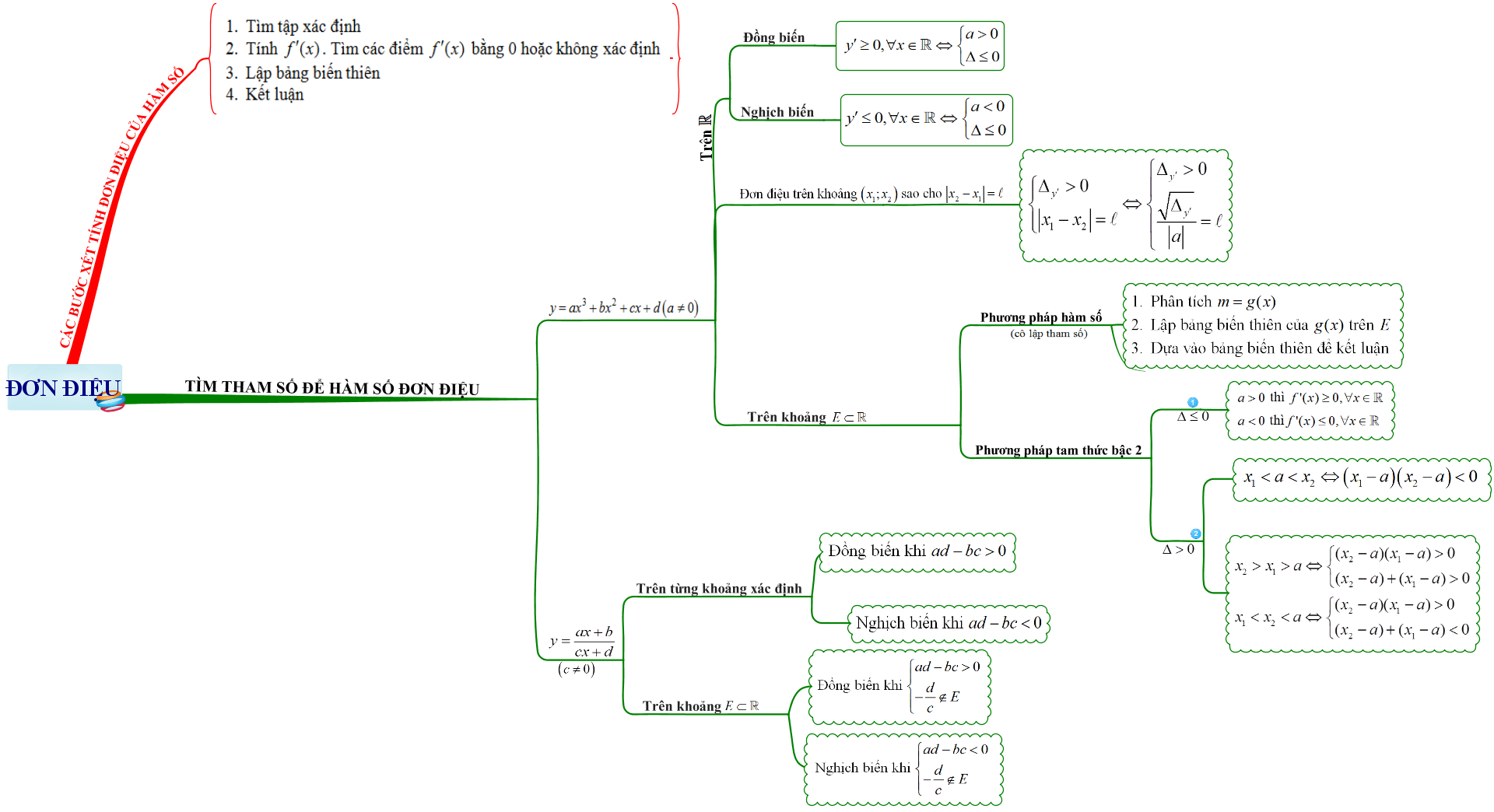
Dạng 1: Xét tính đơn điệu của hàm số

Các bước xét tính đơn điệu của một hàm số cho trước

Bước 1: Tìm tập xác định của hàm số y = f(x)

Bước 2: Tính đạo hàm f'(x) và tìm các điểm xo sao cho f'(xo) = 0 hoặc f'(xo) không xác định.

Bước 3: Lập bảng xét dấu và đưa ra kết luận

160 câu trắc nghiệm hàm số lớp 12 có đáp án

Dạng 2: Từ bảng biến thiên, từ đồ thị hàm y =f(x) số đọc khoảng đơn điệu

Dạng 3: Từ bảng xét dấu, đồ thị của y’ đọc khoảng đơn điệu

+ Nếu từ bảng xét dấu của y’ thì đọc khoảng đơn điệu như sau:
– Trên những khoảng y’ mang dấu + thì hàm đồng biến
– Hàm nghịch biến trên những khoảng y’ mang dấu –

+ Nếu bài cho đồ thị của y’ thì từ đồ thị đó lập lại thành bảng xét dấu và đưa về dạng trên
Các bạn làm như vậy nhiều lần sẽ quen, những bài sau chỉ cần nhìn đồ thị là đọc được không cần lập lại bảng biến thiên.

Lập bảng biến thiên theo quy tắc sau:
– Những vị trí mà đồ thị cắt trục Ox là những điểm y’ = 0
– Những khoảng mà phần đồ thị ở phía trên trục Ox thì y’ dương
– Những khoảng mà phần đồ thị ở phía dưới trục Ox thì y’ âm

Dạng 4: Tìm tham số m để hàm số đơn điệu trên khoảng cho trước

Bài toán 1: TÌm m để hàm phân thức đơn điệu trên các khoảng xác định

(y = ax + b/cx + d và y = atanx + b/ctanx + d)

Bài toán 2: Tìm m để hàm phân thức đơn điệu trên khoảng cho trước

Bài toán 3: Tìm m để hàm bậc 3 đơn điệu trên R, trên khoảng cho trước

Dạng 5: Tìm tham số m để hàm số đơn điệu trên khoảng có độ dài cho trước

Các dạng toán tìm cực trị của hàm số thi THPTQG

Dạng 1. Tìm cực trị của hàm số.

Bài toán 1. Tìm cực trị của hàm số từ biểu thức f(x) hay f'(x).

+ Vấn đề 1. Cho biểu thức f(x), hỏi cực trị của hàm số y = f(x).
+ Vấn đề 2. Cho biểu thức f'(x), hỏi cực trị của hàm số y = f(u(x)) + v(x).

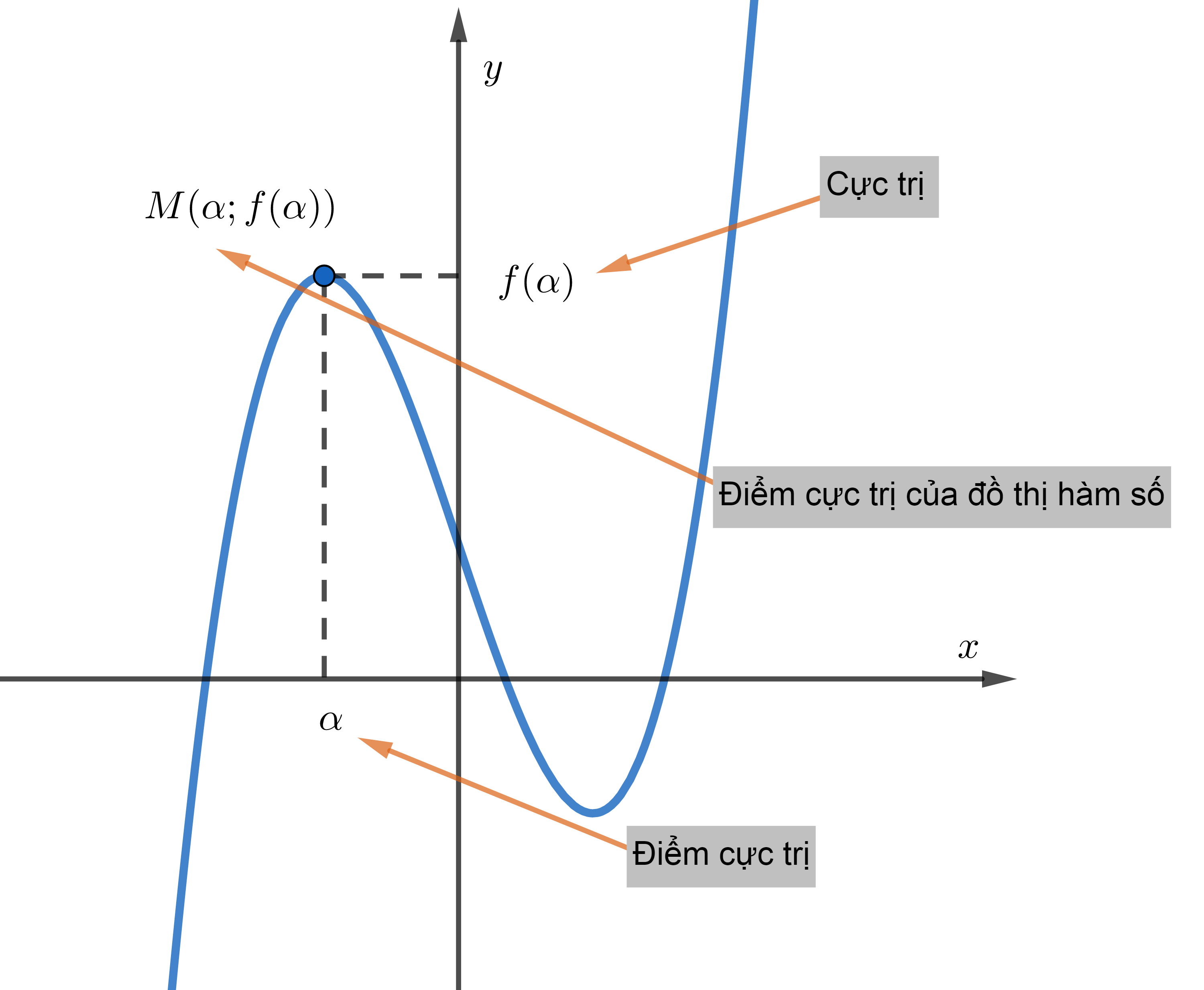
Các dạng toán tìm cực trị của hàm số thi THPTQG

Bài toán 2. Tìm cực trị của hàm số từ bảng biến thiên hay bảng xét dấu f'(x).

+ Vấn đề 1. Cho bảng biến thiên của hàm số y = f(x), hỏi cực trị của hàm số y = f(x).
+ Vấn đề 2. Cho bảng biến thiên của hàm số y = f(x), hỏi cực trị của hàm số y = f(u(x)) + v(x).

Bài toán 3. Từ đồ thị hàm số (C): y = f(x) suy ra điểm cực trị.

+ Vấn đề 1. Cho đồ thị hàm số y = f(x), hỏi cực trị của hàm số y = f(x).
+ Vấn đề 2. Cho đồ thị hàm số y = f(x), hỏi cực trị của hàm số y = f(u(x)) + v(x).

Bài toán 4. Từ đồ thị hàm số (C): y = f'(x), suy ra cực trị của hàm số.

+ Vấn đề 1. Cho đồ thị hàm số y = f'(x), hỏi cực trị của hàm số y = f(x).
+ Vấn đề 2. Cho đồ thị hàm số y = f'(x), hỏi cực trị của hàm số y = f(u(x)).
+ Vấn đề 3. Cho đồ thị hàm số y = f'(x), hỏi cực trị của hàm số y = f(u(x)) + v(x).

Dạng 2. Cực trị hàm chứa tham số

Bài toán 1: Tìm m để hàm số có cực trị
Bài toán 2: Tìm m để hàm số đạt cực trị (cực đại, cực tiểu) tại x = x0
Bài toán 3: Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước (trái dấu, cùng dấu, viet..)

Dạng 3. Cực trị của hàm số có chứa dấu trị tuyệt đối.

Bài toán 1. Tìm số điểm cực trị của hàm số y = |f(x)|.

+ Vấn đề 1. Từ biểu thức của f(x), tìm số điểm cực trị của hàm số y = |f(x)|.
+ Vấn đề 2. Từ biểu thức của f(x) hay f'(x) tìm số điểm cực trị của hàm số y = |f(u(x))| + v(x).
+ Vấn đề 3. Cho bảng biến thiên, hỏi điểm cực trị của hàm số y = |f(u(x)) – a| + v(x), a ∈ R.
+ Vấn đề 4. Cho cho đồ thị của hàm số y = f(x), hỏi điểm cực trị của hàm số y = |f(u(x)) – a| + v(x), a ∈ R.
+ Vấn đề 5. Cho cho đồ thị của hàm số y = f'(x), hỏi điểm cực trị của hàm số y = |f(u(x)) – a| + v(x), a ∈ R.
+ Vấn đề 6. Tìm điều kiện của để hàm số y = |f(u(x)) – v(x)| có n điểm cực trị.

Bài toán 2. Tìm số điểm cực trị của hàm số y = f(|x|).

+ Vấn đề 1. Từ biểu thức của f(x) hay f'(x) tìm số điểm cực trị của hàm số y = f(|ax + b| – c) + d (a, b, c, d ∈ R).
+ Vấn đề 2. Cho bảng biến thiên của hàm số y = f(x) hay bảng xét dấu đạo hàm, hỏi cực trị của hàm số y = f(|ax + b| + c) + d.
+ Vấn đề 3. Cho đồ thị của hàm số y = f(x) hay đồ thị của hàm số y = f'(x), hỏi điểm cực trị của hàm số y = f(|ax + b| + c) + d.
+ Vấn đề 4. Tìm điều kiện của tham số m để hàm số y = f(|x|,m) có n điểm cực trị.

Cách giải các dạng toán tìm max min hàm số lớp 12

1. Cho công thức của y hoặc y’, tìm max min

Sử dụng 1 trong 2 cách ở phía trên

2. Cho bảng biến thiên của y, tìm max min

3. Cho đồ thị hàm số y = f(x), tìm max min trên đoạn

Lưu ý: Điểm cao nhất của đồ thị trên tập K, gióng vào trục Oy sẽ đọc được giá trị lớn nhất, ngược lại với điểm thấp nhất gióng vào Oy ta được giá trị nhỏ nhất.

4. Tìm giá trị lớn nhất nhỏ nhất của hàm số lượng giác

Phương pháp chung:

B1: Biến đổi về 1 hàm số lượng giác

B2: Đặt biến phụ t, tìm tập giá trị của t

B3: Đưa về dạng 1 tìm max min của hàm số.

5. Tìm m để hàm số có giá trị lớn nhất (nhỏ nhất) trên đoạn [a; b] bằng số cho trước

Bước 1: Tính đạo hàm y’ (có chứa m)

Bước 2: Cho y’ = 0, tìm điểm tới hạn xi

Bước 3: Tính f(a); f(b); f(i)

Bước 4: Tùy từng giá trị của m, xác định max, min là giá trị nào; giải pt để tìm m

Phân bậc mức độ:

+ Hàm phân thức B1/B1 đơn giản nhất, vì trên từng khoảng xác định, hàm số luôn đồng biến hoặc nghịch biến.

Vì vậy việc xác định trong các số f(a), f(b), f(xi) đâu là max, min đều dễ dàng

+ Hàm bậc 3, bậc 4 mức độ phức tạp sẽ tăng lên khi ta khó xác định được đâu là max, min

+ Hàm chứa dấu giá trị tuyệt đối phức tạp nhất.