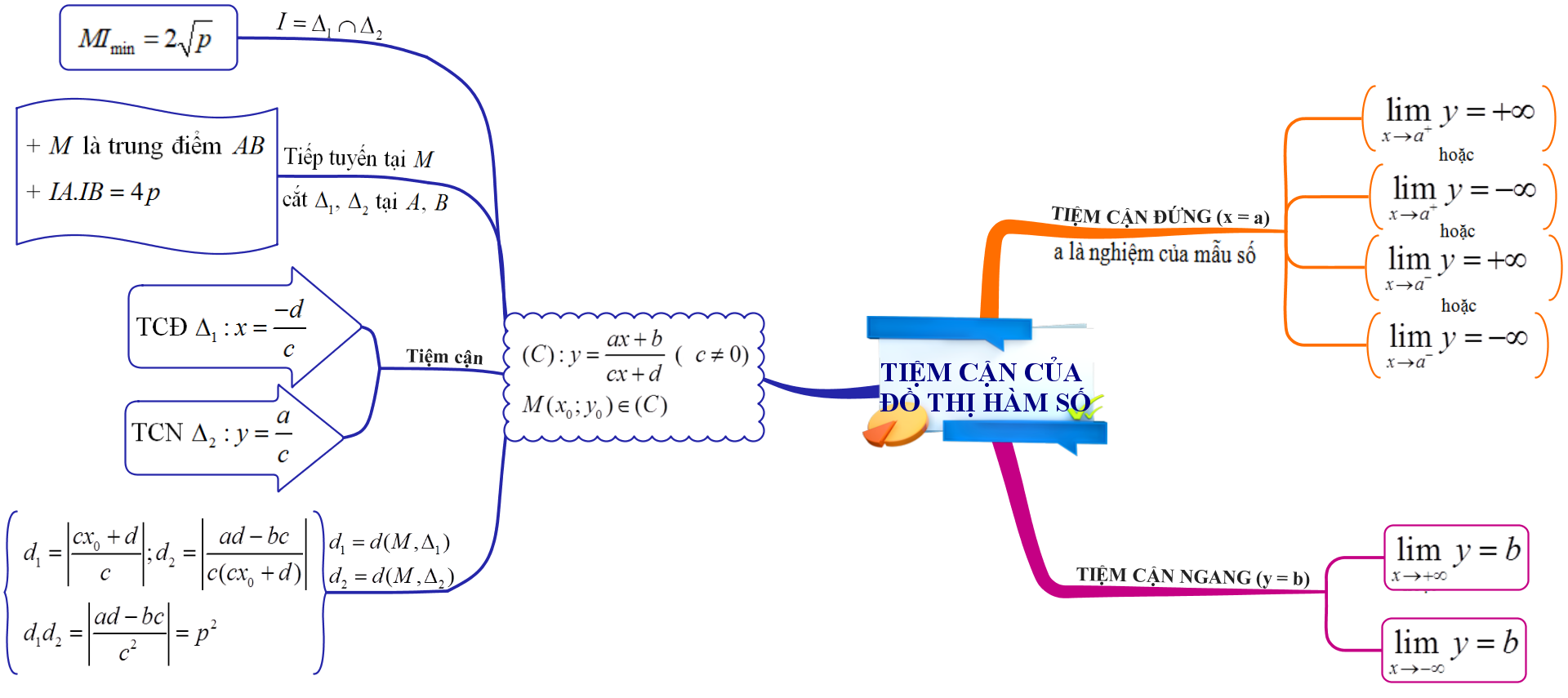
1. Đường tiệm cận ngang – tiệm cận là gì?
2. Đường tiệm cận đứng
Dạng 1: Xác định tiệm cận của đồ thi hàm số cho bởi công thức y = f(x)
+ Hàm phân thức B1/B1
+ Hàm phân thức khác:
Tìm tiệm cận đứng:
– Nghiệm của mẫu không phải nghiệm của tử là tiệm cận đứng. Nếu nghiệm của tử cũng là nghiệm của mẫu thì bấm máy tính lim, kết quả ra vô cực thì đó mới là TCĐ.
– Với hàm chứa căn, phải tính giới hạn
Tìm tiệm cận ngang: Phương pháp chung: Tính giới hạn tại vô cực
Mẹo
– Bậc của tử = Bậc của mẫu => Hàm số có tiệm cận ngang
– Bậc của tử < Bậc của mẫu => Hàm số có tiệm cận ngang y = 0
– Bậc của tử > Bậc của mẫu => Hàm số không có tiệm cận ngang
![]()
Tìm tiệm cận của hàm số chứa căn
Tử hoặc mẫu có chứa căn thức thì:
– Tìm TXĐ trước, nếu TXĐ không chứa vô cực thì không có tiệm cận ngang; Nếu TXĐ không chứa nghiệm của mẫu thì đó không phải là tiệm cận đứng.
– Nếu TXĐ có vô cực thì nên sử dụng máy tính để tìm tiệm cận ngang cho quen, dần dần các em sẽ tự rút ra được quy luật để nhìn nhanh tiệm cận ngang của những hàm loại này.
– Nếu tử chứa căn, khi tìm TCĐ ta tìm nghiệm của mẫu, nếu đó không là nghiệm của tử và thuộc TXĐ thì chắc chắn là TCĐ, nếu nghiệm đó cũng là nghiệm của tử thì tốt nhất bấm máy kiểm tra, kết quả ra vô cực thì đó là TCĐ.
Dạng 2: Cho bảng biến thiên, xác định tiệm cận
+ Nhìn các vị trí của x mà y không xác định, nếu tại đó giá trị của y là vô cực thì đó là tiệm cận đứng.
+ Nhìn vào vị trí x bằng vô cực, nếu ở đó y có giá trị hữu hạn thì đó là tiệm cận ngang (1 hoặc 2 tiệm cận ngang)
![]()
Dạng 3: Cho đồ thị hàm số y = f(x), xác định tiệm cận
![]()
Dạng 4: Tìm m để hàm số có n đường tiệm cận
Phương pháp:
+ Thường thì sẽ có sẵn 1 hoặc 2 tiệm cận ngang, chỉ tìm số tiệm cận đứng hoặc ngược lại
+ Sử dụng mẹo như dạng 1 đưa về bài toán tìm m để đa thức có n nghiệm khác số nào đó.
Dạng 5: Tiệm cận hàm hợp (khó nhất)
Bài tập trắc nghiệm về tiệm cận của đồ thị

Bài viết khác cùng mục: