Phương pháp nguyên hàm từng phần thường được sử dụng để tìm tích phân bất định của các hàm số phức tạp như vừa chứa hàm vô tỉ và hàm lượng giác, hoặc chứa hàm logarit và hàm vô tỉ, hay hàm mũ,…
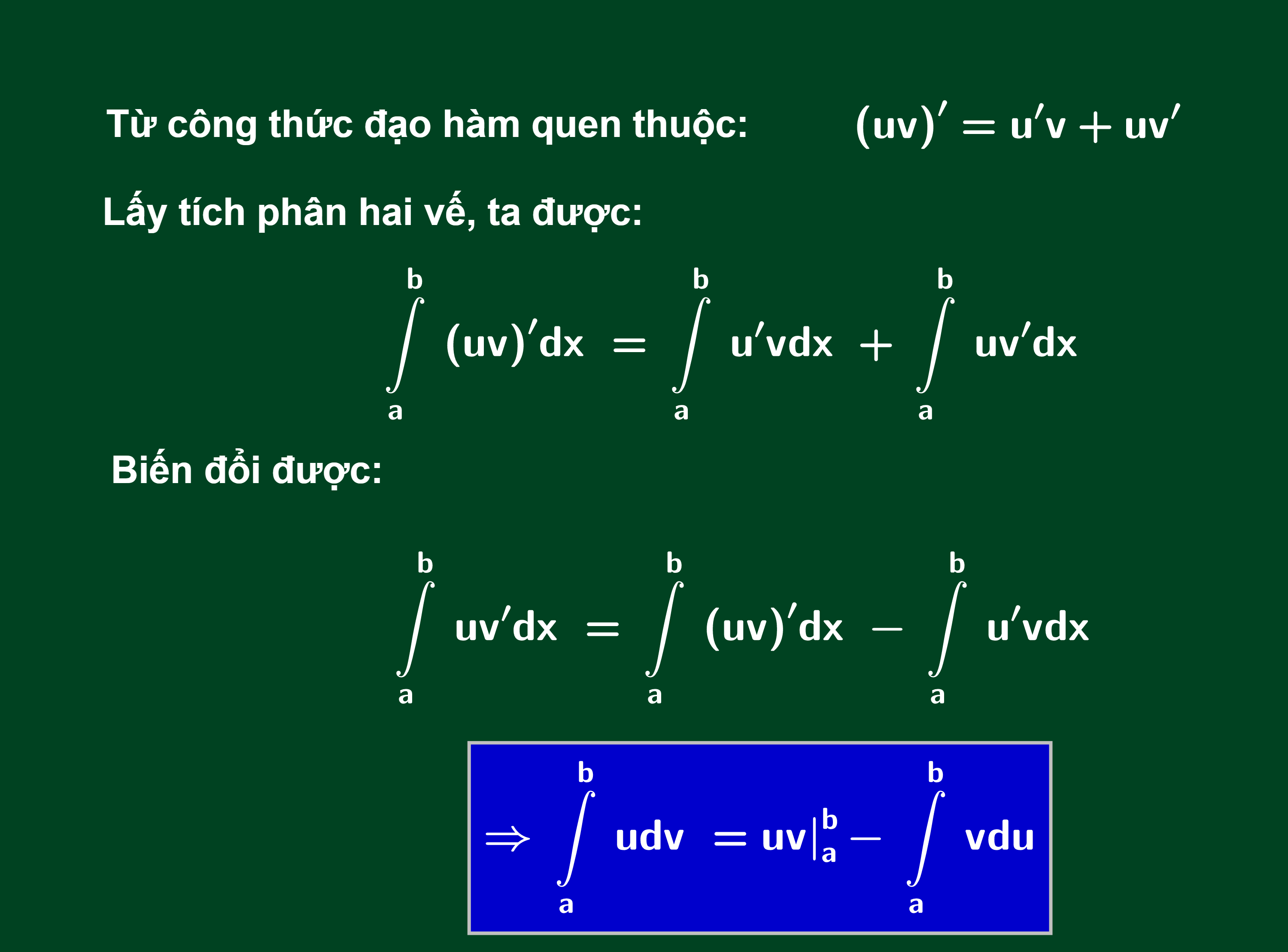
Nguyên hàm từng phần là gì?
Cho hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K ta có công thức nguyên hàm từng phần:
∫udv = uv−∫vdu.
Chú ý: Ta thường sử dụng phương pháp nguyên hàm từng phần nếu nguyên hàm có dạng I=∫f(x).g(x)dx, trong đó f(x) và g(x) là 2 trong 4 hàm số: Hàm số logarit, hàm số đa thức, hàm số lượng giác, hàm số mũ.
Cách tính nguyên hàm từng phần
Bảng nguyên hàm từng phần

Tính nhanh nguyên hàm từng phần bằng sơ đồ – Nguyên hàm từng phần múa cột
![]()
![]()
![]()
Bài tập nguyên hàm từng phần
1. Đề bài
2. Đáp án

Bài viết khác cùng mục: