Phương pháp hàm số giải phương trình Mũ Logarit thi THPTQG

Đăng ngày bởi VanLoan | 1569 Views

Xem nhiều tuần qua:

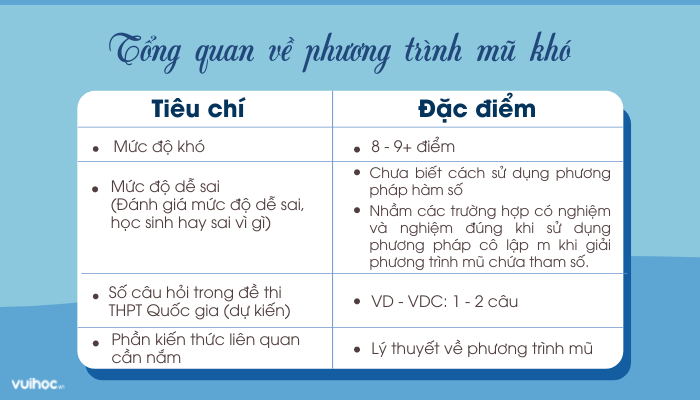
Giải phương trình Mũ Logarit bằng phương pháp hàm số thi THPTQG

Giải phương trình Mũ Logarit bằng phương pháp hàm số thi THPTQG
Giải phương trình Mũ Logarit bằng phương pháp hàm số thi THPTQG

Phương pháp 1: Đưa về cùng cơ số – Phương trình mũ logarit cơ bản

\[\begin{array}{l}
0 < a \ne 1\\
{a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Leftrightarrow f\left( x \right) = g\left( x \right)\\
{a^{f\left( x \right)}} = b \Leftrightarrow f\left( x \right) = {\log _a}b\\
{\log _a}f\left( x \right) = {\log _a}g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}
f\left( x \right) = g\left( x \right)\\
f\left( x \right) > 0
\end{array} \right.\\
{\log _a}f\left( x \right) = b \Leftrightarrow \left\{ \begin{array}{l}
f\left( x \right) = {a^b}\\
f\left( x \right) > 0
\end{array} \right.
\end{array}\]

Phương pháp 2: Logarit hóa phương trình mũ

(với những bài không đưa về cùng cơ số được)

\[\begin{array}{l}
{a^{f\left( x \right)}} = {b^{g\left( x \right)}}\\
\Leftrightarrow {\log _a}{a^{f\left( x \right)}} = {\log _a}{b^{g\left( x \right)}}\\
\Leftrightarrow f\left( x \right) = g\left( x \right).{\log _a}b
\end{array}\]

(Lấy logarit cơ số a hoặc b của 2 vế)

Ví dụ 1: Giải phương trình \[{2^{{x^2} – 4}} = {7^{x – 2}}\]

Giải:

Lấy logarit cơ số 2 cả 2 vế ta được:

\[\begin{array}{l}
{\log _2}{2^{{x^2} – 4}} = {\log _2}{7^{x – 2}}\\
\Leftrightarrow {x^2} – 4 = \left( {x – 2} \right){\log _2}7\\
\Leftrightarrow \left( {x – 2} \right)\left( {x + 2 – {{\log }_2}7} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x – 2 = 0\\
x + 2 – {\log _2}7
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2\\
x = {\log _2}7 – 2
\end{array} \right.
\end{array}\]

Ví dụ 2: Giải phương trình \[{8^x}{.5^{{x^2} – 1}} = {2^{ – 3}}\]

Giải:

Lấy logarit cơ số 8 cả 2 vế ta được: 

\[\begin{array}{l}
{\log _8}{8^x}{.5^{{x^2} – 1}} = {\log _8}\frac{1}{8}\\
\Leftrightarrow {\log _8}{8^x} + {\log _8}{5^{{x^2} – 1}} = {\log _8}{8^{ – 1}}\\
\Leftrightarrow x + \left( {{x^2} – 1} \right){\log _8}5 = – 1\\
\Leftrightarrow x + 1 + \left( {{x^2} – 1} \right){\log _8}5 = 0\\
\Leftrightarrow \left( {x + 1} \right)\left[ {1 + \left( {x – 1} \right){{\log }_8}5} \right] = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = – 1\\
x{\log _8}5 = {\log _8}5 – 1
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = – 1\\
x = \frac{{{{\log }_8}5 – 1}}{{{{\log }_8}5}}
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = – 1\\
x = 1 – {\log _5}8
\end{array} \right.
\end{array}\]

Phương pháp 3: Đặt ẩn phụ

Loại 1: Phương trình dạng \[m.{a^{2f\left( x \right)}} + n.{a^{f\left( x \right)}} + p = 0\]

Đặt \[t = {a^{f\left( x \right)}}{\rm{ }}\left( {t > 0} \right)\]

Ta được phương trình : \[m{t^2} + nt + p = 0\]

Loại 2: Phương trình dạng \[m.{a^{f\left( x \right)}} + n.{b^{f\left( x \right)}} + p = 0\] với \[a.b = 1\]

Đặt \[t{\rm{ = }}{a^{f\left( x \right)}}{\rm{ }}\left( {t > 0} \right)\] \[ \Rightarrow {b^{f\left( x \right)}} = \frac{1}{t}\]

Loại 3: Phương trình dạng \[m.{a^{2f\left( x \right)}} + n.\left( {a.{b^{f\left( x \right)}}} \right) + p.{b^{2f\left( x \right)}} = 0\]

Chia 2 vế cho \[{b^{2f\left( x \right)}}\]

Đặt \[t = {\left( {\frac{a}{b}} \right)^{f\left( x \right)}}{\rm{ }}\left( {t > 0} \right)\]

Ta được phương trình : \[m{t^2} + nt + p = 0\]

Phương pháp 4: Đặt ẩn phụ không hoàn toàn

Ví dụ 1: Giải phương trình \[{3.4^x} + \left( {3x – 10} \right){2^x} + 3 – x = 0\]

Giải: 

Đặt \[t = {2^x}{\rm{ }}\left( {t > 0} \right)\]

Ta được phương trình: \[3{t^2} + \left( {3x – 10} \right)t + 3 – x = 0\]

Có \[\Delta = {\left( {3x – 10} \right)^2} – 12\left( {3 – x} \right) = {\left( {3x – 8} \right)^2}\]

\[ \Rightarrow (1) \Leftrightarrow \left[ \begin{array}{l}
t = \frac{1}{3}\\
t = – x + 3
\end{array} \right.\]

Với \[t = \frac{1}{3} \Rightarrow {2^x} = \frac{1}{3} \Leftrightarrow x = – {\log _2}3\]

Với  \[\begin{array}{l}
t = – x + 3 \Rightarrow {2^x} + x = 3\\
\Leftrightarrow x = 1
\end{array}\] ( Do vế trái là hàm đồng biến, vế phải không đổi nên có tối đa 1 nghiệm, nhẩm được x = 1)

Phương pháp 5: Giải phương trình mũ bằng phương pháp hàm số

Cách 1 – Phương pháp đánh giá hàm số

    • Bước 1. Chuyển phương trình về dạng f(x)=k.
 
    • Bước 2. Khảo sát sự biến thiên của hàm số f(x) trên D. Khẳng định hàm số đơn điệu
 
    • Bước 3. Nhẩm nghiệm \[x = {x_0}\]
 
    • Bước 4. Kết luận vậy x = x0 là nghiệm duy nhất của phương trình.
 

Cách 2

    • Bước 1. Chuyển phương trình về dạng f(x) = g(x).
 
    • Bước 2. Khảo sát sự biến thiên của hàm số y = f(x) và y = g(x). Khẳng định hàm số y = f(x) là hàm số đồng biến còn y = g(x) là hàm số nghịch biến hoặc là hàm hằng.
 
    • Bước 3. Nhẩm nghiệm \[x = {x_0}\]
 
    • Bước 4. Kết luận vậy \[x = {x_0}\] là nghiệm duy nhất của phương trình.
 

Cách 3

    • Bước 1. Chuyển phương trình về dạng f(u) = f(v).
 
    • Bước 2. Khảo sát sự biến thiên của hàm số y = f(x). Khẳng định hàm số đơn điệu.
 
    • Bước 3. Khi đó f(u) = f(v) ⇔ u = v.

Ví dụ minh họa

Ví dụ 1: Giải phương trình: \[{4^x} + {5^x} = 9\]
 
Giải: 
+ Nhẩm được x = 1 là nghiệm của phương trình
+ Chứng minh đó là nghiệm duy nhất:
Xét hàm số \[f\left( x \right) = {4^x} + {5^x}\]
Có \[f’\left( x \right) = {4^x}.\ln 4 + {5^x}.\ln 5 > 0{\rm{ }}\forall x \in \]
=> Hàm số đồng biến trên R
Vế phải là hằng số nên phương trình có tối đa 1 nghiệm.
 
Ví dụ 2: Giải phương trình \[x + \sqrt {{x^2} + 1} = {5^x}\]
 
Giải : 
Lấy ln hai vế ta được :
\[\begin{array}{l}
\ln \left( {x + \sqrt {{x^2} + 1} } \right) = \ln {5^x}\\
\Leftrightarrow \ln \left( {x + \sqrt {{x^2} + 1} } \right) – x.\ln 5 = 0
\end{array}\]
Xét hàm số \[f\left( x \right) = \ln \left( {x + \sqrt {{x^2} + 1} } \right) – x.\ln 5\]
Có 
\[f’\left( x \right) = \frac{1}{{\sqrt {{x^2} + 1} }} – \ln 5 < 0\]
(vì \[\begin{array}{l}
\frac{1}{{\sqrt {{x^2} + 1} }} < 1;{\rm{ }}\ln 5 > 1\\
\Rightarrow \frac{1}{{\sqrt {{x^2} + 1} }} < \ln 5
\end{array}\] )
+ Nhẩm được x = 0 là nghiệm, vậy đó là nghiệm duy nhất.
 
Ví dụ 3: Giải phương trình \[3.{x^{{{\log }_3}x}} + {\left( {{{\log }_3}x – 1} \right)^2} = {x^2}\]
 
Giải: 
Đặt \[t = {\log _3}x \Leftrightarrow x = {3^t}\]
Ta được phương trình:
\[\begin{array}{l}
3.{\left( {{3^t}} \right)^t} + {\left( {t – 1} \right)^2} = {3^{2t}}\\
\Leftrightarrow {3^{{t^2} + 1}} + {t^2} + 1 = {3^{2t}} + 2t{\rm{ (1)}}
\end{array}\]
Xét hàm số \[f(u) = {3^u} + u\]
Có \[f’\left( u \right) = {3^u}\ln 3 + 1 > 0{\rm{ }}\forall u \in \]
=>Hàm số đồng biến trên R, khi đó:
\[\begin{array}{l}
\left( 1 \right) \Leftrightarrow f\left( {{t^2} + 1} \right) = f\left( {2t} \right)\\
\Leftrightarrow {t^2} + 1 = 2t\\
\Leftrightarrow t = 1\\
\Rightarrow {\log _3}x = 1 \Leftrightarrow x = 3
\end{array}\]

Phiếu Bài tập phương trình mũ Logarit

Like share và ủng hộ chúng mình nhé: