Các dạng toán trắc nghiệm tìm cực trị của hàm số thi THPTQG
Dạng 1. Tìm cực trị của hàm số.
Bài toán 1. Tìm cực trị của hàm số từ biểu thức f(x) hay f'(x).
+ Vấn đề 1. Cho biểu thức f(x), hỏi cực trị của hàm số y = f(x).
+ Vấn đề 2. Cho biểu thức f'(x), hỏi cực trị của hàm số y = f(u(x)) + v(x).
Bài toán 2. Tìm cực trị của hàm số từ bảng biến thiên hay bảng xét dấu f'(x).
+ Vấn đề 1. Cho bảng biến thiên của hàm số y = f(x), hỏi cực trị của hàm số y = f(x).
+ Vấn đề 2. Cho bảng biến thiên của hàm số y = f(x), hỏi cực trị của hàm số y = f(u(x)) + v(x).
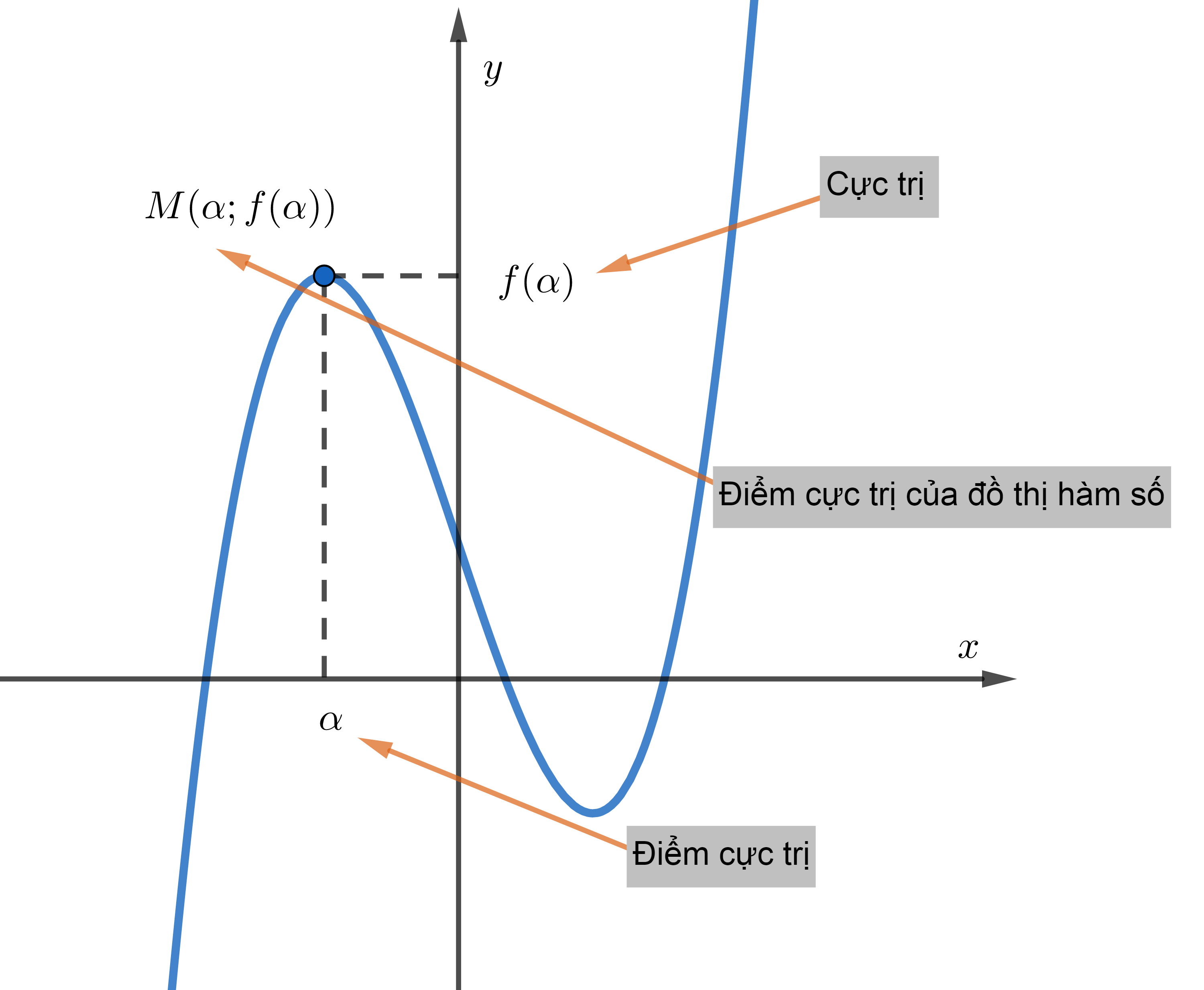
Bài toán 3. Từ đồ thị hàm số (C): y = f(x) suy ra điểm cực trị.
+ Vấn đề 1. Cho đồ thị hàm số y = f(x), hỏi cực trị của hàm số y = f(x).
+ Vấn đề 2. Cho đồ thị hàm số y = f(x), hỏi cực trị của hàm số y = f(u(x)) + v(x).
Bài toán 4. Từ đồ thị hàm số (C): y = f'(x), suy ra cực trị của hàm số.
+ Vấn đề 1. Cho đồ thị hàm số y = f'(x), hỏi cực trị của hàm số y = f(x).
+ Vấn đề 2. Cho đồ thị hàm số y = f'(x), hỏi cực trị của hàm số y = f(u(x)).
+ Vấn đề 3. Cho đồ thị hàm số y = f'(x), hỏi cực trị của hàm số y = f(u(x)) + v(x).
![]()
Dạng 2. Cực trị hàm chứa tham số
Bài toán 1: Tìm m để hàm số có cực trị
Bài toán 2: Tìm m để hàm số đạt cực trị (cực đại, cực tiểu) tại x = x0
Bài toán 3: Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước (trái dấu, cùng dấu, viet..)
Dạng 3. Cực trị của hàm số có chứa dấu trị tuyệt đối.
Bài toán 1. Tìm số điểm cực trị của hàm số y = |f(x)|.
+ Vấn đề 1. Từ biểu thức của f(x), tìm số điểm cực trị của hàm số y = |f(x)|.
+ Vấn đề 2. Từ biểu thức của f(x) hay f'(x) tìm số điểm cực trị của hàm số y = |f(u(x))| + v(x).
+ Vấn đề 3. Cho bảng biến thiên, hỏi điểm cực trị của hàm số y = |f(u(x)) – a| + v(x), a ∈ R.
+ Vấn đề 4. Cho cho đồ thị của hàm số y = f(x), hỏi điểm cực trị của hàm số y = |f(u(x)) – a| + v(x), a ∈ R.
+ Vấn đề 5. Cho cho đồ thị của hàm số y = f'(x), hỏi điểm cực trị của hàm số y = |f(u(x)) – a| + v(x), a ∈ R.
+ Vấn đề 6. Tìm điều kiện của để hàm số y = |f(u(x)) – v(x)| có n điểm cực trị.
![]()
Bài toán 2. Tìm số điểm cực trị của hàm số y = f(|x|).
+ Vấn đề 1. Từ biểu thức của f(x) hay f'(x) tìm số điểm cực trị của hàm số y = f(|ax + b| – c) + d (a, b, c, d ∈ R).
+ Vấn đề 2. Cho bảng biến thiên của hàm số y = f(x) hay bảng xét dấu đạo hàm, hỏi cực trị của hàm số y = f(|ax + b| + c) + d.
+ Vấn đề 3. Cho đồ thị của hàm số y = f(x) hay đồ thị của hàm số y = f'(x), hỏi điểm cực trị của hàm số y = f(|ax + b| + c) + d.
+ Vấn đề 4. Tìm điều kiện của tham số m để hàm số y = f(|x|,m) có n điểm cực trị.
Bài tập cực trị hàm số có hướng dẫn

Bài viết khác cùng mục: