Cách giải các dạng toán tìm max min hàm số lớp 12
2 cách tìm max min hàm số trên tập K sử dụng đạo hàm
Cách 1: Lập bảng biến thiên
(Sử dụng với các bài lượng giác hoặc tập K không phải là đoạn [a; b])
Bước 1. Tính đạo hàm f'(x).
Bước 2. Tìm các nghiệm của f'(x) và các điểm f'(x)trên K.
Bước 3. Lập bảng biến thiên của f(x) trên K.
Bước 4. Căn cứ vào bảng biến thiên kết luận
Cách 2: Không dùng bảng biến thiên – Giá trị lớn nhất của hàm số trên đoạn
(Dùng với các bài cơ bản, tập K là đoạn [a; b])
Bước 1. Tính đạo hàm f'(x).
Bước 2. Tìm tất cả các nghiệm xi ∈[a; b] của phương trình f'(x) = 0 và tất cả các điểm αi ∈ [a; b] làm cho f'(x) không xác định.
Bước 3.Tính f(a), f(b), f(xi), f(αi).
Bước 4. So sánh các giá trị tính được và kết luận
Các dạng toán tìm max min của hàm số
1. Cho công thức của y hoặc y’, tìm max min
Sử dụng 1 trong 2 cách ở phía trên
2. Cho bảng biến thiên của y, tìm max min
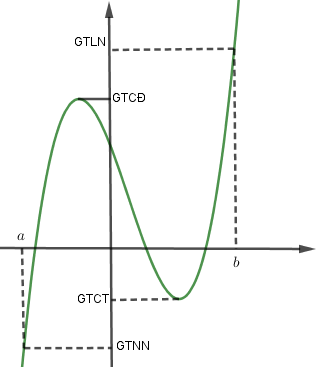
3. Cho đồ thị hàm số y = f(x), tìm max min trên đoạn
Lưu ý: Điểm cao nhất của đồ thị trên tập K, gióng vào trục Oy sẽ đọc được giá trị lớn nhất, ngược lại với điểm thấp nhất gióng vào Oy ta được giá trị nhỏ nhất.
4. Tìm giá trị lớn nhất nhỏ nhất của hàm số lượng giác
Phương pháp chung:
B1: Biến đổi về 1 hàm số lượng giác
B2: Đặt biến phụ t, tìm tập giá trị của t
B3: Đưa về dạng 1 tìm max min của hàm số.
5. Tìm m để hàm số có giá trị lớn nhất (nhỏ nhất) trên đoạn [a; b] bằng số cho trước
Bước 1: Tính đạo hàm y’ (có chứa m)
Bước 2: Cho y’ = 0, tìm điểm tới hạn xi
Bước 3: Tính f(a); f(b); f(i)
Bước 4: Tùy từng giá trị của m, xác định max, min là giá trị nào; giải pt để tìm m
Phân bậc mức độ:
+ Hàm phân thức B1/B1 đơn giản nhất, vì trên từng khoảng xác định, hàm số luôn đồng biến hoặc nghịch biến.
Vì vậy việc xác định trong các số f(a), f(b), f(xi) đâu là max, min đều dễ dàng
+ Hàm bậc 3, bậc 4 mức độ phức tạp sẽ tăng lên khi ta khó xác định được đâu là max, min
+ Hàm chứa dấu giá trị tuyệt đối phức tạp nhất.
Bài tập trắc nghiệm Max min của hàm số đủ 4 mức độ có giải

Bài viết khác cùng mục: