Công thức ứng dụng tích phân tính diện tích, thể tích đầy đủ
1. Ứng dụng tích phân tính diện tích hình phẳng
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thẳng x = a, x = b được xác định: $$S = \int\limits_a^b {\left| {f\left( x \right)} \right|} dx$$
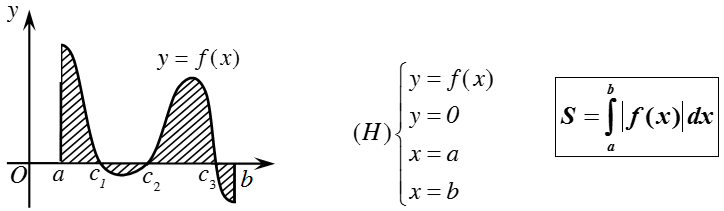
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a, x = b được xác định: : $$S = \int\limits_a^b {\left| {f\left( x \right) – g\left( x \right)} \right|} dx$$
Chú ý:
– Nếu trên đoạn [a; b], hàm số f(x) không đổi dấu thì: $$\int\limits_a^b {\left| {f\left( x \right)} \right|} dx = \left| {\int\limits_a^b {f\left( x \right)dx} } \right|$$
– Diện tích của hình phẳng giới hạn bởi các đường x = g(y), x = h(y) và hai đường thẳng y = c, y = d được xác định: $$S = \int\limits_c^d {\left| {g\left( y \right) – h\left( y \right)} \right|} dy$$
2. Thể tích vật thể và thể tích khối tròn xoay
a) Thể tích vật thể:
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x, (a ≤ x ≤ b). Giả sử S(x) là hàm số liên tục trên đoạn [a; b].
Khi đó, thể tích của vật thể B được xác định: $$V = \int\limits_a^b {S\left( x \right)} dx$$
b) Thể tích khối tròn xoay:
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x) , trục hoành và hai đường thẳng x = a, x = b quanh trục Ox:
Chú ý:
– Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x = g(y), trục hoành và hai đường thẳng y = c, y = d quanh trục Oy:
– Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x), y = g(x) và hai đường thẳng x = a, x = b quanh trục Ox: $$V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) – {g^2}\left( x \right)} \right|} dx$$
Kĩ năng giải bài tập
1. Câu hỏi tính diện tích hình phẳng giới hạn bởi các đường:
Những điểm cần lưu ý:
Trường hợp 1. Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi các đường y = f(x), y = g(x), x = a, x = b là $$S = \int\limits_a^b {\left| {f\left( x \right) – g\left( x \right)} \right|} dx$$
Phương pháp giải toán
+) Giải phương trình f(x) = g(x)
+) Nếu (1) vô nghiệm thì $$S = \left| {\int\limits_a^b {\left( {f\left( x \right) – g\left( x \right)} \right)dx} } \right|$$
+) Nếu (1) có nghiệm thuộc .[a; b]. giả sử α thì $$S = \left| {\int\limits_a^\alpha {\left( {f\left( x \right) – g\left( x \right)} \right)dx} } \right| + \left| {\int\limits_\alpha ^b {\left( {f\left( x \right) – g\left( x \right)} \right)dx} } \right|$$
Chú ý: Có thể lập bảng xét dấu hàm số trên đoạn rồi dựa vào bảng xét dấu để tính tích phân.
Trường hợp 2. Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi các đường y = f(x), y = g(x) là $$S = \int\limits_\alpha ^\beta {\left| {f\left( x \right) – g\left( x \right)} \right|} dx$$
Trong đó α, β là nghiệm nhỏ nhất và lớn nhất của phương trình f(x) = g(x) (a ≤ α < β ≤ b).
Phương pháp giải toán
Bước 1. Giải phương trình f(x) = g(x) tìm các giá trị α, β.
Bước 2. Tính $$S = \int\limits_\alpha ^\beta {\left| {f\left( x \right) – g\left( x \right)} \right|} dx$$ như trường hợp 1.
2. Câu hỏi tính tính thể tích vật tròn xoay giới hạn bởi các đường:
Những điểm cần lưu ý:
. Tính thể tích khối tròn xoay:
Trường hợp 1. Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = a và x = b (a < b) quay quanh trục Ox là $$V = \pi \int\limits_a^b {{f^2}\left( x \right)} dx$$
Trường hợp 2. Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y = f(x), y = g(x), x = a và x = b (a < b) quay quanh trục Ox là $$V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) – {g^2}\left( x \right)} \right|} dx$$

Bài viết khác cùng mục: